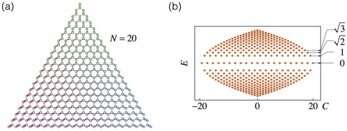
a. SL with site-varying coupling strengths. b. Energy spectrum of the FSL. Credit: Science China Press
Since the discovery of the quantum Hall effect, topological phases of electrons have become a major research area in condensed matter physics. Many topological phases are predicted in lattices with specific engineering of electronic hopping between lattice sites. Unfortunately, the distance between neighboring sites in natural lattices (crystals) is on the order of a billionth of a meter, which makes such engineering extremely difficult. On the other hand, the photonic crystals have a much larger scale. The unit cells of photonic crystals for visible light are several thousand times larger than those of electrons. Therefore, it is not surprising that people resort to photonic analog of topological phases by digging out the similarity between the Maxwell and Schrodinger equations, and a research area named topological photonics has flourished.
However, photons and electrons are as different as dogs and cats. Photons are social by nature. They love to stay together (this is why we have lasers). Electrons hate each other. They have their own territories according to the Fermi exclusion principle. Topological photonics based on the analog between the Maxwell and Schrodinger equations belongs to classical optics, i.e., a classical-wave simulation of the electronic band topology. It is natural to ask whether quantized light embeds new topological phases beyond the interpretation of classical optics. Recently, Han Cai and Da-Wei Wang from Zhejiang University revealed the topological phases in lattices of quantized states of light.
The energy of light can only exist in discrete packs, a non-negative integer plus one half of hν, where h is the Planck constant and ν is the frequency of light. The integer is the number of photons in that state, which is called the Fock state, and the one half is contributed by the vacuum fluctuations. This discreteness of light energy is the key to explain the spectra of the black-body radiation (e.g., in a furnace, higher temperature shifts the spectra to the blue side of a rainbow strip). Light quantization also has profound consequence in atom-photon interactions. When there are n photons in the light field, the probability for an excited atom to emit another photon is proportional to n+1 (remember that photons are social and they love new members to join in). When light is confined in a cavity, the energy emitted by the atom can be reabsorbed, which results in an oscillation of the atom between the excited and ground states, and the oscillation frequency is proportional to the square root of n+1. A spectrum of these discrete values of the oscillation frequencies can be observed when the atom is coupled with light in a superposition of Fock states, i.e., in the Jaynes-Cummings (JC) model, which has become a standard method in obtaining the quantum states of light.
It is not obvious that the JC model is related to topological phases, but this square-root-of-integer scaling of the energy spectrum is in reminiscence of the Landau levels of electrons in a graphene, which is a cradle of topological phases. The energy bands of electrons in a graphene touches at two points on the edge of the Brillouin zone, named the Dirac points, where the electrons obeying the two-dimensional Dirac equation have a linear relation between its energy and momentum. When a magnetic field is applied, the electrons make cyclotron motions with discrete frequencies scaling with the square root of integers, which correspond to discrete Landau levels. Cai and Wang established the connection between the three-mode JC model and the Dirac electrons in a magnetic field.
In a three-mode JC model where an atom is coupled to three cavity modes, the quantum states can be fully described by four integers (x, y, z, q), where x, y and z are the photon numbers in the three cavity modes, and q=0 and 1 for the ground and excited states of the atom. In the JC model, all the (N+1)^2 states satisfying x+y+z+q=N form a honeycomb lattice, similar to a graphene and we call it the Fock-state lattice. Since the excited atom can emit a photon to one of the cavity modes, the state (x, y, z, 1) is coupled to three neighboring states, (x+1, y, z, 0), (x, y+1, z, 0) and (x, y, z+1, 0). However, the coupling strengths to the three cavity modes are proportional to the square root of their photon numbers. For each state (x, y, z, 1) there is a competition between the three cavities to obtain the photon emitted by the atom, and the cavities that contain more photons have an advantage, which can be understood as the majority principle of photons. This is equivalent to a graphene subjected to a strain which modifies the hopping coefficients of electrons from one site to its three neighbors.
It turns out that when the coupling strength between the most populous cavity mode and the atom is larger than the summation of those of the other two modes, the two Dirac points merge and a band gap opens, which is a Lifshitz topological transition between a semimetal and a band insulator. In the semimetallic phase, the variation of the coupling strength is equivalent to a strain field which induces an effective magnetic field and leads to quantized Landau levels, based on which the authors investigated the valley Hall effect and built a Haldane model in the three-mode JC model.
The authors also investigated the one-dimensional Fock-state lattices with only two cavity modes. They are intrinsic Su-Schriefer-Heeger models and host topological edge states. The model can be further extended to higher than three dimensions for topological phases unavailable in real lattices. The proposed topological phases are ready to be realized in superconducting circuits and are promising for applications in quantum information processing.
More information: Han Cai et al, Topological phases of quantized light, National Science Review (2020). DOI: 10.1093/nsr/nwaa196
Provided by Science China Press