Synthetic dimensions enable a new way to construct higher-order topological insulators
Topological insulators have been an exciting field of research with fundamental interest as well as practical applications such as robust transport of electrons and light, and topological quantum computing. The hallmark of such conventional topological insulators is the presence of conducting boundary modes which have one dimension lower than the insulating bulk system that hosts them—for example a one-dimensional edge mode at the boundary of a two-dimensional system, or a two-dimensional surface state at the boundary of a three-dimensional system. In 2017, scientists generalized this concept to predict a new phase of matter called higher-order topological insulators (HOTIs), which support 'corner modes'—e.g. a zero-dimensional mode in a two-dimensional system. Since then, there have been several experimental demonstrations of this new HOTI phase, most of which involve complicated geometries. Moreover, these previous systems are fixed—i.e. one cannot dynamically switch or tune their higher-order topological behavior once they are fabricated.
In a new paper published in Light Science & Applications, a team of scientists, led by Professor Shanhui Fan from Stanford University, USA, and co-workers have proposed a way to realize such higher-order topology and corner states using an emerging concept called 'synthetic dimensions,' in simpler structures and in a dynamically tunable way. Usually, particles like photons and electrons are assumed to move along the three directions—x, y and z, or length, width and depth. What if one could imagine the motion of photons beyond these three 'real' directions? The team calls these extra directions of motion 'synthetic dimensions.'
To make this conceptual leap from the three real dimensions to synthetic dimensions, they harnessed internal properties inherent to all photons—the frequency or color of light, which determines how much energy a photon carries. Previous work from the Stanford team and other groups have demonstrated conventional (first-order) topological phases using this concept of synthetic dimensions, including intriguing physical phenomena such as the quantum Hall effect. However, higher-order topology had remained beyond the reach of synthetic dimensions till now, although the high-dimensional nature of HOTIs is very well suited to the idea of synthetic dimensions.
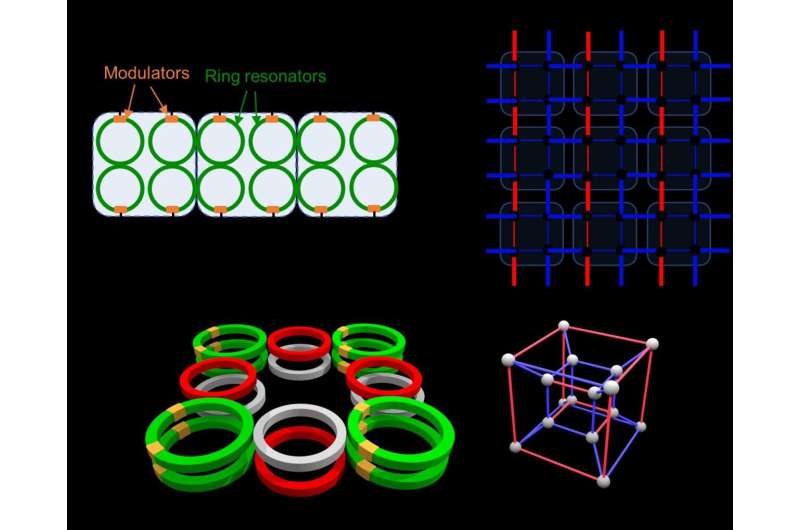
To construct the higher-order topological insulator, the researchers propose using a set of ring resonators which are coupled to each other in a specific arrangement. Each ring resonator is essentially a thin wire of a transparent material looped on itself, such that a photon can go around the loop many times. A pair of two identical ring resonators together forms a 'photonic molecule,' just like two hydrogen atoms form a diatomic molecule. By arranging multiple such photonic molecules along a line, a second-order topological insulator for photons can be formed. Just like in real dimensions one can control whether a photon moves to the right or the left (say in the x direction), the ring resonator can control in synthetic dimensions whether a photon moves up or down in frequency. Such movement in frequency is achieved with another photonic component called a modulator—a device that can change the material's refractive index at high speeds, making them essential to today's optical telecommunications networks.
Next, the team predicts how the hallmark of higher-order topology—the corner modes—can be seen in this system by sending specific frequencies of laser light into the set of photonic molecules. For these corner modes, light is confined to the corner of the two-dimensional structure consisting of one real dimension and one synthetic frequency dimension, and there is almost no light in the rest of the structure.
"A big advantage of synthetic dimensions is the flexibility with which various knobs can be controlled to tune system parameters. By controlling the strength and timing of the electronic signal applied to the modulators in the photonic molecules, we showed how these corner modes could be turned on and off. In other words, you can switch the system from having higher-order topology to having no topology, dynamically. This capability is unmatched in typical electronic or photonic systems," the authors say.
With synthetic dimensions, one can think of building very high-dimensional topological insulators, which are difficult to build or even imagine in real space because we live in a three-dimensional world. As an example, the team constructs a fourth-order topological insulator in a four-dimensional system, which has not been predicted before since it is beyond the purview of three-dimensional real space.
"Our recipes lay out how to use synthetic dimensions to implement very complicated high-dimensional phenomena, including extremely-high-order topological insulators and other exotic phases of light and matter, in much simpler systems, and dynamically control their properties almost at will. Experimental realizations of this concept are well within the reach of current state-of-the-art photonic technology," the scientists add.
More information: Avik Dutt et al, Higher-order topological insulators in synthetic dimensions, Light: Science & Applications (2020). DOI: 10.1038/s41377-020-0334-8
Journal information: Light: Science & Applications
Provided by Chinese Academy of Sciences