Credit: CC0 Public Domain
Quantum computing promises to improve our ability to perform some critical computational tasks in the future. Machine learning is changing the way we use computers in our present everyday life and in science. It is natural to seek connections between these two emerging approaches to computing, in the hope of reaping multiple benefits. The search for connecting links has just started, but we are already seeing a lot of potential in this wild, unexplored territory. We present here two new research articles: "Precise measurement of quantum observables with neural-network estimators," published in Physical Review Research, and "Fermionic neural-network states for ab-initio electronic structure," published in Nature Communications.
Taming the wave function
Today, the prediction of electronic structure properties for molecules and materials is thought to be one of the shortest paths to quantum advantage.
Simulating quantum mechanics, on the other hand, is a brand-new application for the sharpest tool of machine learning: neural networks. Only in recent years have neural networks been used to classify phases of quantum matter or as variational ansatz for interacting many body systems.
Representing quantum wave functions is something that both quantum computers and neural networks strive to do. This common ground can be used as a starting point for the exploration of possible connections. Each approach has its advantages, and its weak points.
The importance of being precise
The variational quantum eigensolver (VQE), together with other low-depth algorithms for electronic structure, exploits storage and manipulation of quantum states to retrieve ground and excited state properties of quantum systems of interest. To do that, for the case of molecular systems, we need to measure the expectation value of Hamiltonian operators, which represent molecular energies. We also need to do that very precisely: a measurement with heavy random fluctuations would make the whole quantum algorithm unusable for practical purposes. As it turns out, quantum computers are not very good at this task. More specifically, the number of measurements to achieve enough precision for applications that would show quantum advantage is prohibitive for current technology.
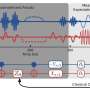
In PRR's "Precise measurement of quantum observables with neural-network estimators," a collaboration with two researchers from the Flatiron Institute, Giacomo Torlai and Giuseppe Carleo, we used neural network techniques on quantum computing for more-accurate chemistry simulations. The technique is based on the training of a neural network, with measurement data gathered on a quantum computer. Once trained, the neural network encodes a partial representation of the quantum state, which is good enough to recover molecular energies with extreme precision.
A quantum computer, integrated with our new neural-network estimator, combines the advantages of the two approaches.
A quantum computer, integrated with our new neural-network estimator, combines the advantages of the two approaches. While a quantum circuit of choice is being executed, we exploit the power of quantum computers to interfere states over an exponentially-growing Hilbert space. After the quantum interference process has worked its course, we obtain a finite collection of measurements. Then a classical tool—the neural network—can use this limited amount of data to still efficiently represent partial information of a quantum state, such as its simulated energy.
This handing of data from a quantum processor to a classical network leaves us with the big question:
How good are neural networks at capturing the quantum correlations of a finite measurement dataset, generated sampling molecular wave functions?
Quantum computing toolbox for computational scientists
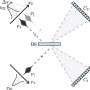
To answer this question, we had to think about how neural network could emulate fermionic matter. Neural networks had been used so far for the simulation of spin lattice and continuous-space problems. Solving fermionic models with neural network remained an elusive task. To find a way around that, we looked into the way molecules are simulated on quantum computers.
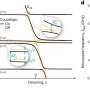
We used encodings of fermionic degrees of freedom to qubit ones, which are the very same encodings used when carrying out molecular simulations on quantum computers, as in variational algorithms. With these mappings, available on Qiskit Aqua, we have defined fermionic neural network states. We tested them on a classical computer, against molecular ground states, which are quantum objects of practical interest for both quantum and classical computations.
In the Nature Communications article from May, 2020, written with Kenny Choo (University of Zurich) and Giuseppe Carleo (Flatiron Institute), we have shown that shallow neural networks such as restricted Boltzmann machines can capture ground state energies of small molecular systems, using variational Monte Carlo techniques.
The results of this work impact both quantum and classical computing. In fact, on the one hand, our work suggests that we can safely train neural networks on quantum data from molecular systems. On the other hand, we have shown that quantum computing tools, such as fermion-to-qubit encodings, can be used in the context of classical computational techniques.
These links will further bolster mutual interactions between the classical computational science and quantum computing communities. For quantum computing, it may mean that future applications in the quantum simulation space will increasingly benefit from processing of quantum data by machine learning techniques. For computational physics and chemistry, it is time to start looking at what can be learned from quantum computing algorithms.
More information: Giacomo Torlai et al. Precise measurement of quantum observables with neural-network estimators, Physical Review Research (2020). DOI: 10.1103/PhysRevResearch.2.022060
Kenny Choo et al. Fermionic neural-network states for ab-initio electronic structure, Nature Communications (2020). DOI: 10.1038/s41467-020-15724-9
Journal information: Nature Communications
Provided by IBM