Scientists at the UK's National Physical Laboratory (NPL) have performed the most accurate measurement yet of the Boltzmann constant.
While the impact of such an achievement is not immediately obvious, the measurement could revolutionise the way we define temperature, replacing the standard method that has been used for over 50 years.
The new measurement is 1.380 651 56 (98) × 10?23 J K?1, where the (98) shows the uncertainty in the last two digits, which amounts to an uncertainty of 0.7 parts per million —almost half the previous lowest uncertainty.
The result has been published today, 11 July, in the journal Metrologia by IOP Publishing on behalf of the Bureau International des Poids et Mesures (BIPM).
Scientists currently define the kelvin and the degree Celsius using the temperature of the triple point of water – the point at which liquid water, solid ice and water vapour can all exist in equilibrium.
This 'standard temperature' has been defined as 273.16 K exactly. The temperature measurements we make in everyday life are an assessment of how much hotter or colder an object is compared to this value.
As temperature measurements need to be made with increasing accuracy across a wide range of disciplines, fixing a single temperature as a standard becomes problematic, especially when you're measuring extremely hot or cold temperatures.
Lead author of the study, Dr Michael de Podesta, said: The further away one measures from the temperature of the triple point of water, the harder it gets to precisely determine the ratio of exactly how much hotter or colder the temperature is than the standard temperature. This adds uncertainty to temperature measurements on top of the normal practical difficulties."
The solution is to redefine the kelvin using a fixed constant of nature, just as the metre has moved from a physical piece of metal to the length of the path travelled by light in vacuum over a specified number of nanoseconds. The suggested method is to use the Boltzmann constant, which is a measure of the relationship between the kinetic energy of molecules and temperature.
"It is fascinating that we worked out how to measure temperature long before we knew what temperature actually was. Now we understand that the temperature of an object is related to the energy of motion of its constituent atoms and molecules. When you touch an object and it feels 'hot' you are literally sensing the 'buzzing' of the atomic vibrations. The new definition directly links the unit of temperature to this basic physical reality," continued de Podesta.
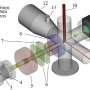
In this study, the researchers, in collaboration with Cranfield University and the Scottish Universities Environmental Research Centre (SUERC), used acoustic thermometry to make the measurement by building an acoustic resonator and making amazingly precise measurements of the speed of sound in argon gas.
The researchers first cooled the resonator to the temperature of the triple point of water so they knew the temperature exactly in the current definition and filled it with argon gas that had its isotopic purity assessed by the SUERC team.
Then they used the speed of sound measurement to calculate the average speed of the argon molecules and hence the average amount of kinetic energy that they had – from this they were able to calculate the Boltzmann constant with an extremely high accuracy.
In order to achieve this high accuracy, the researchers also needed to measure the radius of the resonator with a high accuracy.
The team at Cranfield University used a single-crystal diamond cutting tool to produce four copper hemispheres. The best pair, when put together, formed a triaxially-ellipsoidal resonator that was the correct shape to within one thousandth of a millimetre. The radius was then calculated using the specific frequencies at which the wavelength of microwaves exactly fit into the resonator and was measured with an overall uncertainty of 11.7 nm, which is the thickness of about 600 atoms.
"This experiment has been exhilarating, and after six years we are exhausted. Every aspect of the experiment has required pushing science and engineering to the limit. In this kind of work we need to worry constantly about all the things which might go wrong, and how they might affect the results. We are looking forward to worrying a little less and getting on with exploiting some of the new technology we have invented in the course of the project," continued de Podesta.
More information: "A low-uncertainty measurement of the Boltzmann constant" de Podesta M, Underwood R J, Sutton G, Morantz P, Harris P M, Mark D F, Stuart F M, Vargha G and Machin G 2013 Metrologia 50 354-376. iopscience.iop.org/0026-1394/50/4/354
Journal information: Metrologia
Provided by Institute of Physics
.jpg)