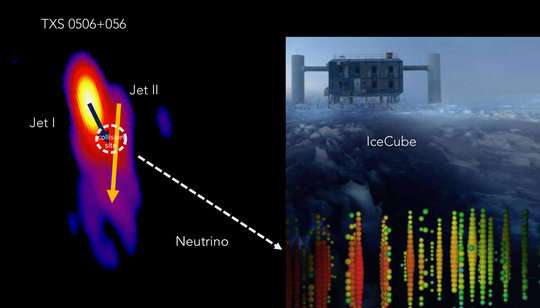
TXS 0506+056. The neutrino event IceCube 170922A appears to originate in the interaction zone of the two jets. Credit: IceCube Collaboration, MOJAVE, S. Britzen, & M. Zajaček
The neutrino event IceCube 170922A, detected at the IceCube Neutrino Observatory at the South Pole, appears to originate from the distant active galaxy TXS 0506+056, at a light travel distance of 3.8 billion light years. TXS 0506+056 is one of many active galaxies and it remained a mystery why and how only this particular galaxy generated neutrinos so far.
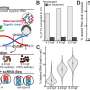
An international team of researchers led by Silke Britzen from the Max Planck Institute for Radio Astronomy in Bonn, Germany, studied high-resolution radio observations of the source between 2009 and 2018, before and after the neutrino event. The team proposes that the enhanced neutrino activity during an earlier neutrino flare and the single neutrino could have been generated by a cosmic collision within TXS 0506+056. The clash of jet material close to a supermassive black hole seems to have produced the neutrinos.
The results are published in Astronomy & Astrophysics, October 02, 2019.
On July 12, 2018, the IceCube collaboration announced the detection of the first high-energy neutrino, IceCube-170922A, which could be traced back to a distant cosmic origin. While the cosmic origin of neutrinos had been suspected for quite some time, this was the first neutrino from outer space whose origin could be confirmed. The 'home' of this neutrino is an Active Galactic Nucleus (AGN)—a galaxy with a supermassive black hole as central engine. An international team could now clarify the production mechanism of the neutrino and found an equivalent to a collider on Earth: a cosmic collision of jetted material.
AGNs are the most energetic objects in our Universe. Powered by a supermassive black hole, matter is being accreted and streams of plasma (so-called jets) are launched into intergalactic space. BL Lac objects form a special class of these AGNs, where the jet is directly pointing at us and dominating the observed radiation. The neutrino event IceCube-170922A appears to originate from the BL Lac object TXS 0506+056, a galaxy at a redshift of z=0.34, corresponding to a light travel distance of 3.8 billion light years. An analysis of archival IceCube data by the IceCube Collaboration had revealed evidence of an enhanced neutrino acitvity earlier, between September 2014 and March 2015.
Other BL Lac Objects show properties quite similar to those of TXS 0506+056. "It was a bit of a mystery, however, why only TXS 0506+056 has been identified as a neutrino emitter," explains Silke Britzen from the Max Planck Institute for Radio Astronomy (MPIfR), the lead author of the paper. "We wanted to unravel what makes TXS 0506+056 special, to understand the neutrino creation process and to localize the emission site and studied a series of high resolution radio images of the jet."
Much to their surprise, the researchers found an unexpected interaction between jet material in TXS 0506+056. While jet plasma is usually assumed to flow undisturbed in a kind of channel, the situation seems different in TXS 0506+056. The team proposes that the enhanced neutrino activity during the neutrino flare in 2014–2015 and the single EHE neutrino. IceCube-170922A could have been generated by a cosmic collision within the source.
This cosmic collision can be explained by new jet material crashing into older jet material. A strongly curved jet structure provides the proper set up for such a scenario. Another explanation involves the collision of two jets in the same source. In both scenarios, it is the collision of jetted material which generates the neutrino. Markus Böttcher from the North-West University in Potchefstroom (South Africa), a co-author of the paper, performed the calculations with regard to the radiation and particle emission. "This collision of jetted material is currently the only viable mechanism which can explain the neutrino detection from this source. It also provides us with important insight into the jet material and solves a long-standing question whether jets are leptonic, consisting of electrons and positrons; or hadronic, consisting of electrons and protons; or a combination of both. At least part of the jet material has to be hadronic—otherwise, we would not have detected the neutrino."
In the course of the cosmic evolution of our Universe, collisions of galaxies seem to be a frequent phenomenon. Assuming that both galaxies contain central supermassive black holes, the galactic collision can result in a black hole pair at the centre. This black hole pair might eventually merge and produce the supermassive equivalent to stellar black hole mergers as detected in gravitational waves by the LIGO/Virgo collaboration.
AGNs with double black holes at a small separation of only light years have been pursued for many years. However, they seem to be rare and difficult to identify. In addition to the collision of jetted material, the team also found evidence for a precession of the central jet of TXS 0506+056. According to Michal Zajaček from the Center for Theoretical Physics, Warsaw: "This precession can in general be explained by the presence of a supermassive black hole binary or the Lense-Thirring precession effect as predicted by Einstein's theory of general relativity. The latter could also be triggered by a second, more distant black hole in the centre. Both scenarios lead to a wandering of the jet direction, which we observe."
Christian Fendt from the Max Planck Institute for Astronomy in Heidelberg is amazed: "The closer we look at the jet sources the more complicated the internal structure and jet dynamics appears. While binary black holes produce a more complex outflow structure, their existence is naturally expected from the cosmological models of galaxy formation by galaxy mergers."
Silke Britzen stresses the scientific potential of the findings: "It's fantastic to understand the neutrino generation by studying the insides of jets. And it would be a breakthrough if our analysis had provided another candidate for a binary black hole jet source with two jets."
It seems to be the first time that a potential collision of two jets on scales of a few light years has been reported and that the detection of a cosmic neutrino might be traced back to a cosmic jet-collision.
While TXS 0506+056 might not be representative of the class of BL Lac objects, this source could provide the proper setup for a repeated interaction of jetted material and the generation of neutrinos.
More information: S. Britzen et al. A cosmic collider: Was the IceCube neutrino generated in a precessing jet-jet interaction in TXS 0506+056?, Astronomy & Astrophysics (2019). DOI: 10.1051/0004-6361/201935422
Journal information: Astronomy & Astrophysics
Provided by Max Planck Society