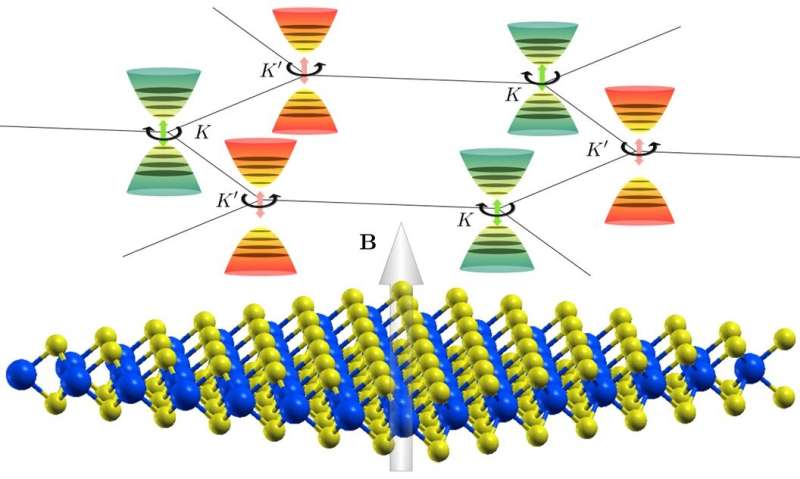
The figure shows the crystal structure of a 2D transition metal dichalcogenide (bottom) with the inequivalent valleys (K and K’) representing the different momenta of electrons in the material (top). In the presence of a magnetic field (denoted by B), the energies of electronic states at the respective valleys are shifted by the Zeeman effect, and the states reorganise to form quantised Landau levels in each valley. Electronic states at each valley (orange and green) couple to light that is circularly polarised in one direction. Credit: Quek Su Ying
NUS researchers have developed a parameter-free approach to quantitatively predict the response of two-dimensional (2-D) valleytronics materials to an external magnetic field. These predictions are important because they provide insights into the many-body effects into a fascinating property of these materials that enables the magnetic field to increase the stability of one valley (bit "one") over the other (bit "zero").
Valleytronics is now being actively considered as another new paradigm for information processing, following its predecessors, "electronics" and "spintronics." Valleytronics involves manipulating the momentum of the electron, which depends on which of two inequivalent valleys (see Figure) the electron belongs to.
2-D transition metal dichalcogenides (TMDs) that lack inversion symmetry are particularly promising for valleytronics, because the spin and valley degrees of freedom are inextricably linked. This implies that an external magnetic field can be used as a knob to tune the stability of one valley over the other to distinguish bits. Furthermore, the bits can be read using optical measurements. This is because light that is circularly polarized in the clockwise direction can only be absorbed and emitted from one of these valleys, and vice versa for light that is circularly polarized in the anticlockwise direction. The confluence of these intriguing properties has resulted in many experimental efforts to measure the response of TMDs to external magnetic fields.
Quantum mechanics says that when an external magnetic field is applied to a periodic crystal, the original electronic states reorganize to form quantised levels, called Landau levels, which give rise to the quantum Hall effect, where the Hall conductance takes on quantized values. At the same time, the energy levels also shift linearly with the applied magnetic field strength, in what is known as the Zeeman effect.
In this work, Prof Quek Su Ying from the Department of Physics, NUS and her postdoctoral fellow, Dr. Xuan Fengyuan, built on an approach developed in 1951 by renowned physicist, J.M. Luttinger, to derive expressions for the energy levels of 2-D TMDs in the presence of a weak external magnetic field. The resulting expressions captured both the Landau levels and the Zeeman effect on an equal footing and use a completely general Hamiltonian in contrast to previous studies, and the resulting energy levels are in good quantitative agreement with the Landau levels predicted from optical measurements.
The quantum mechanical calculations show for the first time that non-local many-body effects are important to explain the experimentally observed Zeeman effect of interlayer exciton energies in twisted bilayer TMDs. The researchers also predicted that each Landau level is associated with a unique electron spin and valley index, which demonstrates clearly the potential of these 2-D materials for valleytronic applications.
Prof Quek said, "This development is a much-needed step toward achieving a clearer understanding of the effects of magnetic fields on 2-D TMDs. This is critical to enable rational design and control of the relative stability of the two logical bits in valleytronics applications for 2-D TMDs and their heterostructures. There is still much to explore to gain a more complete understanding of the complex interactions of electrons with magnetic fields in these intriguing 2-D materials."
More information: Fengyuan Xuan et al. Valley Zeeman effect and Landau levels in two-dimensional transition metal dichalcogenides, Physical Review Research (2020). DOI: 10.1103/PhysRevResearch.2.033256
Provided by National University of Singapore