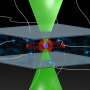
Artist's rendering of the inner structure of a proton showing quarks and quark-antiquark pairs, with springs showing the gluons that bind the quarks. Image courtesy of Klaus Rith
(PhysOrg.com) -- At a meeting this week of the American Physical Society in Washington, MIT Associate Professor of Physics Bernd Surrow reported on new results from the STAR experiment at the Relativistic Heavy Ion Collider (RHIC) that provide a better understanding of the internal structure of the proton, the basic building block of all nuclei.
The world’s only polarized proton collider, at Brookhaven National Laboratory in Upton, N.Y., RHIC is used by MIT physicists to understand how the proton gets its spin, a fundamental quantum mechanical property (spin manifests itself as an intrinsic magnetic field, a property that is the basis of magnetic resonance imaging, or MRI). In 2009, spin-polarized protons were collided in RHIC at a record high center-of-mass energy of 500 giga electron volts (GeV). At this high energy — an energy 250 times the mass of the two individual protons making the collision — the protons are moving essentially at the speed of light and the quarks inside the proton are able to “see” each other at a resolution that is very small compared to the size of the proton. This allows scientists to study the proton's internal structure.
Nobody has yet succeeded in performing a decomposition for the proton spin in terms of its constituent quarks and gluons. The accompanying cartoon shows a model of how complicated the “simple” proton actually is; its structure arises through the strong force and is described by the quantum theory of quarks and gluons known as quantum chromodynamics (QCD). This theory has thus far been unable to explain the origin of proton spin, so new insight is obtained from experiments. It has been established that the quarks themselves account for only about 25 percent of the proton’s spin and previous Brookhaven data provided by Surrow’s team indicate that the gluon’s contribution is also small.
Protons have a spin of ½, a number whose simplicity is compelling, considering that the proton is made up of several constituent particles.
The results presented in Washington this week have established a new way to explore the spin structure of the proton by using the weak interaction, which is responsible for radioactive β-decay (a process that converts a neutron into a proton while emitting an electron and an electron antineutrino). The weak interaction is mediated by very massive (about 80 GeV) particles known as W bosons. At RHIC, the longitudinal polarization of the colliding polarized proton beams at high energies allows the experiments to directly observe the weak interactions by detecting the decay electrons of the W bosons produced. This process gives rise to a large parity violating signal. (Parity violation means that physics results are different in processes occurring in left- and right-handed systems.) Such a signal has now been established for the first time by careful measurement of the spin-dependent cross section under the leadership of Surrow's group at the MIT Laboratory for Nuclear Science. The STAR experiment is well suited to carry out such measurements because of its large acceptance for the detection of the decay electron produced by the W boson. In addition, it can discriminate against background processes from the strong interaction.
The production of W bosons provides an ideal tool to study the quark spin structure of the proton. W bosons are produced in quark-antiquark collisions and can be detected through their respective decay electrons. The analysis distinguishes the electric charge sign of the decay product, which provides a direct view of the quark polarization at high energies where fundamental calculations are well under control. The results from Surrow’s group clearly establish the different polarization patterns of up and down quarks. They are consistent with fundamental calculations within the Standard Model (SM) of particle physics. This new technique allows direct sensitivity to the polarization of anti-quarks.
Surrow’s group is also developing new tracking detectors that will greatly increase the ability to detect the parity-violating W events in further data-taking planned for 2011/2012. These measurements will focus on measuring the polarization of the anti-quarks, which only live fleetingly in the proton.
Provided by Massachusetts Institute of Technology