August 19, 2019 feature
Holography and criticality in matchgate tensor networks
Tensor networks take a central role in quantum physics as they can provide an efficient approximation to specific classes of quantum states. The associated graphical language can also easily describe and pictorially reason about quantum circuits, channels, protocols and open systems. In a recent study, A. Jahn and a research team in the departments of complex quantum systems, materials and energy and mathematics and computer science in Germany introduced a versatile and efficient framework to study tensor networks by extending previous tools. The researchers used bulk tiling (computing geometric technique) in their work to obtain highly accurate critical data and established a link between holographic quantum error-correcting codes and tensor networks. They expect the work to stimulate further investigations of tensor network models to capture bulk-boundary correspondences. The results are now published on Science Advances.
The AdS/CFT correspondence, which stands for anti-de Sitter/conformal field theory correspondence, is one of the largest areas of research in string theory, and is an example in the context of bulk-boundary dualities in which a holographic duality exists between gravity in a bulk space and a critical quantum field on its boundary. This correspondence that relates two very different theories was originally formulated by physicist Juan M. Maldacena in 1997, and is considered a significantly important result in string theory within the last 20 years.
A key feature of these dualities is the relationship between bulk geometry and boundary entanglement entropies, which physicists had previously illuminated using the Ryu-Takayanagi formula. Since it is important to understand entanglement in the context of AdS/CFT, researchers realized the necessity of tensor networks as an ideal framework to construct holographic toy models, such as the multiscale entanglement renormalization ansatz simulation (MERA). Physicists had previously explored the realization that quantum error correction could be facilitated by a holographic duality, which further connected to ideas from quantum information theory. Although researchers did successfully construct several tensor network models to reproduce a variety of aspects on AdS/CFT, they still lacked a general understanding of the features and limits of tensor network holography. Specific obstacles to the process include the potentially large parameter spaces of tensor networks and the considerable computational costs involved.
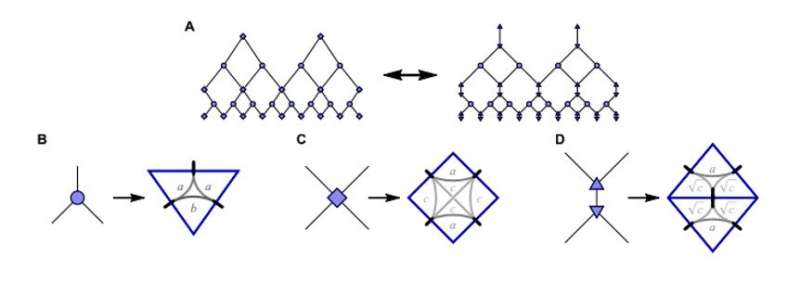
In the present work, Jahn et al. overcame the existing challenges by applying highly efficient contraction techniques developed by matchgate tensors. The versatile techniques allowed the research team to comprehensively study the interplay of geometry and correlations in Gaussian fermionic tensor networks by incorporating toy models of quantum error correction. They also included previous tensor network approaches such as the "MERA' model within the present work, to highlight connections between them. The team restricted the study to tensor networks that are nonunitary and real, resembling a Euclidean evolution from the bulk to boundary. Jahn et al. provided new approaches in the context of tensor network renormalization, to substantiate the capability of tensor networks to describe bulk-boundary correspondences beyond known models. The present work is preliminary and provides a starting point for more systematic studies on holography in tensor networks.
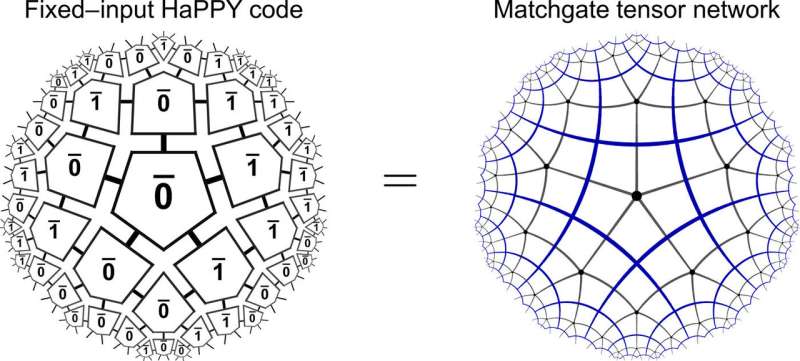
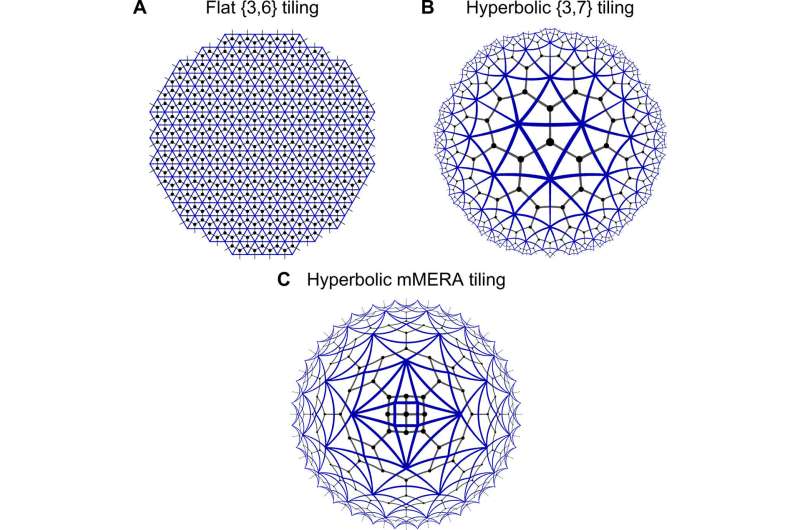
The scientists first applied their framework to the highly symmetric class of regular bulk tilings to implement the holographic error correcting code (HaPPY code) proposed elsewhere. Thereafter, they explored the versatility of the framework to extend it toward more physical setups. They first used the HaPPY code toy model to understand the bulk/boundary correspondence with bulk tiling of holographic pentagons, where each pentagon tile encoded one fault-tolerant logical qubit. Briefly, the research team observed that fixing the bulk degrees of freedom to computational basis states could give rise to a matchgate tensor network. They showed the computational basis states to be pure Gaussian and concluded that for fixed computational input in the bulk, the holographic pentagram code could yield a matchgate tensor on the boundary. Using a Schläfli symbol {p,q} where p = the number of edges per polygon and q = the number of polygons around each corner, they specified the hyperbolic geometry of the HaPPY model.
After Jahn et al. showed their model framework to include the holographic pentagon code built from five-qubit stabilizer states for fixed bulk inputs. They showed the boundary states to correspond to nonlocal bulk pairing with exotic particles known as Majorana fermions. The work thus opened an avenue to study the state properties of a holographic model at large sizes. The scientists further calculated the two-point correlators and entanglement entropies of the system. They then showed that the critical and gapped Gaussian boundary states could be realized beyond known models using various bulk tilings. In the present work they reproduced the average scaling properties of the Ising CFT (conformal field theory) toy model; simplest possible model in theoretical physics that allowed methods of Euclidean quantum field theory and the study of critical phenomena.
-
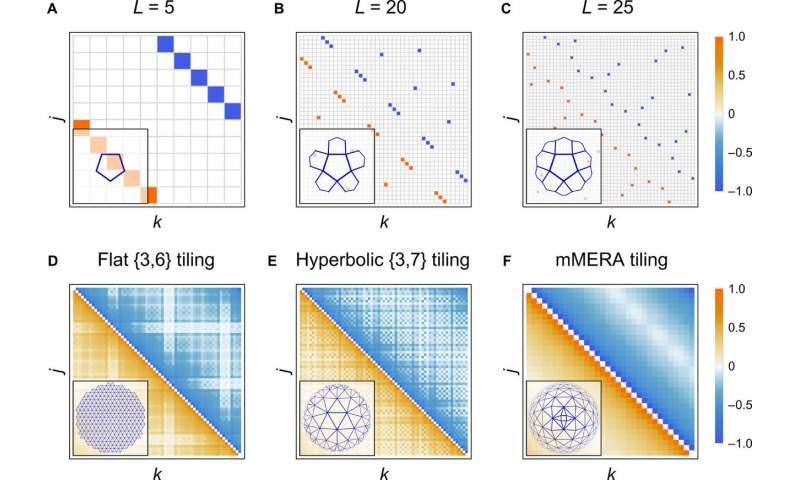
Boundary state correlations. (A to C) Majorana covariance matrix Γ with color-coded entries for a boundary state of a hyperbolic {5,4} tiling of the HaPPY code with fixed 0¯ input on each tile. Boundary consists of 2L = 10, 40, and 50 Majorana sites, respectively. (D to F) Field correlation matrix 〈ψjψk − ψkψj〉/2 = (Γ2j,2k−1 + Γ2j−1,2k)/4 for boundary states of the {3,6}, {3,7}, and mMERA tiling at criticality with L = 63, 69, and 64 boundary sites, respectively. Matrix entries are normalized to the same color scale. The tiling corresponding to each correlation matrix in (A) to (F) is shown in the lower left corner. Credit: Science Advances, doi: 10.1126/sciadv.aaw0092 -
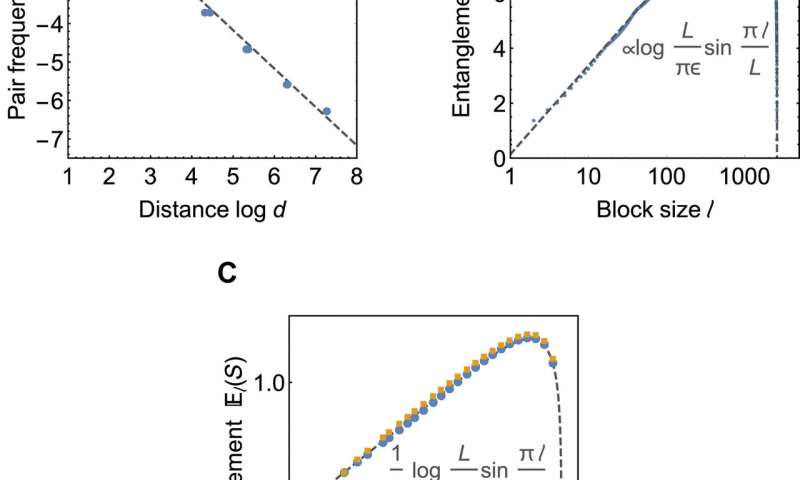
Critical correlations and entanglement scaling. (A and B) Boundary state properties of the HaPPY code at 2605 boundary sites. (A) shows average correlations at boundary distance d, computed as the relative frequency n of Majorana pairs. Dashed gray line shows an n(d)~1/d numerical fit. (B) shows the scaling of average entanglement entropy El(S) with subsystem size l. Dashed gray line shows numerical fit using (11). (C) El(S) for regular tilings at the critical values a = 0.580 for a {3,6} tiling (blue) and at a = 0.609 for the {3,7} tiling (yellow) with 348 boundary sites each. The dashed gray line shows the exact c = 1/2 CFT solution. Credit: Science Advances, doi: 10.1126/sciadv.aaw0092
Jahn et al. then constructed a Euclidean matchgate tensor network based on the previously developed MERA geometry and named it the matchgate MERA (mMERA). This tiling invariance which they expressed as a triangulation (multiple measures to capture a construct), recovered the Ising CFT with little computational cost. The computational optimization process in the study only took a few minutes on a desktop computer for a network with hundreds of tensors.
In this way, A. Jahn and colleagues introduced an efficient preliminary framework to study tensor networks and proposed for further studies within the Gaussian setting to focus on positively curved bulks, higher dimensional models and random tensors. Additional studies beyond Gaussianity could explore interacting fermionic tensor networks by weak-coupling expansion or under locally restricted interactions. Both of the suggested possible extensions of the framework presented in the study will only require computational scaling polynomial to the system size to avoid prohibitive computational efforts of general methods to extract tensor contraction.
More information: A. Jahn et al. Holography and criticality in matchgate tensor networks, Science Advances (2019). DOI: 10.1126/sciadv.aaw0092
Fernando Pastawski et al. Code Properties from Holographic Geometries, Physical Review X (2017). DOI: 10.1103/PhysRevX.7.021022
Vijay Balasubramanian et al. Holographic particle detection, Physical Review D (2002). DOI: 10.1103/PhysRevD.61.044007
Román Orús. A practical introduction to tensor networks: Matrix product states and projected entangled pair states, Annals of Physics (2014). DOI: 10.1016/j.aop.2014.06.013
Journal information: Science Advances , Physical Review X , Physical Review D
© 2019 Science X Network