May 28, 2019 feature
Researchers demonstrate constraints on symmetries from holography
A pair of researchers, one at the Massachusetts Institute of Technology (MIT) and another at California Institute of Technology (Caltech) and the University of Tokyo, have recently investigated a set of old conjectures about symmetries in quantum gravity. The specific conjectures of focus: (1) Quantum gravity does not allow for global symmetries; (2) For gauge symmetry, all possible charges must be realized; (3) Internal gauge groups must be compact. Their paper, published in Physical Review Letters, shows that these old assumptions hold within the anti-de Sitter/conformal field theory (AdS-CFT) correspondence.
"Historically, the concept of symmetry has played important roles in physics, both in identifying and formulating fundamental laws of nature, and in using these laws to understand and predict natural phenomena such as dynamics and phases of matters," Hirosi Ooguri, one of the researchers who carried out the study, told Phys.org. "However, there has been theoretical evidence to suggest that, once we combine gravity and quantum mechanics (the two fundamental ideas in modern physics), all global symmetries are gone."
In physics, symmetries can be of two kinds: gauge and global. For several decades, researchers have proposed the idea that global symmetries should not be possible in quantum gravity, as the unified theory of gravity and quantum mechanics would not allow for any symmetry. This is a profound claim with important consequences. For instance, it predicts that a proton would not be stable against decaying into other particles.
"The standard model of particle physics has both kinds of symmetries, so we are predicting that the global ones must only be approximate," Daniel Harlow, the other researcher involved in the study, told Phys.org. "So far, this idea has had some circumstantial support, but there was no convincing argument. In our paper, we gave what we think is a rather convincing argument in the special case of the AdS/CFT correspondence. This correspondence gives our best-understood theories of quantum gravity, and we were able to show that it does not allow global symmetries."
Prior to Ooguri and Harlow's paper, other researchers made arguments supporting the claim that quantum gravity (the unification of quantum mechanics and gravity) cannot have any symmetry. Nonetheless, these arguments often presented logical gaps or loopholes, for instance failing to address some important cases (e.g. discrete symmetry).
"Our new paper provides a rigorous proof of this claim in the context of the AdS/CFT correspondence, where quantum gravity is defined in a mathematically precise way, and we have done so in the most general way, excluding all possible global symmetries from quantum gravity," Ooguri said.
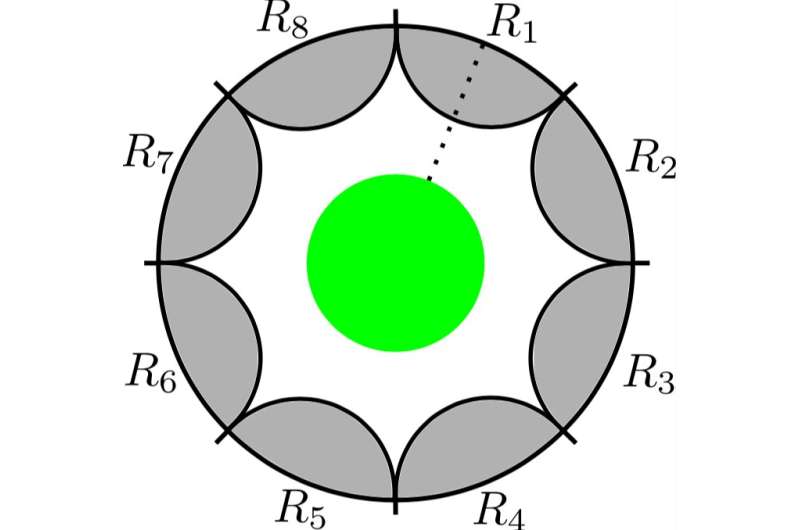
The proof presented by Ooguri and Harlow is based on two important ideas: the holographic principle of quantum gravity and quantum error correcting codes. The holographic principle was first introduced by Gerard 't Hooft and Leonard Susskind in the early '90s, yet it has since been widely built upon. One of its most crucial developments was the discovery of the AdS/CFT correspondence by Juan Maldacena in 1997.
Ooguri and Harlow wished to prove a mathematical theorem on quantum gravity, so they required a precise definition of the holographic principle. They decided to adopt the AdS/CFT correspondence, as this was the only way they felt they could achieve their goal.
"Our basic tools are quantum error correction, the AdS/CFT correspondence, and quantum field theory," Harlow said. "Probably the most important point to convey here is that although AdS/CFT is a beautiful theory of quantum gravity, it is not the theory of quantum gravity in our world. It is a toy model of the type that physicists like to study (such as the famous spherical cow). We believe, however, that lessons we learn in this toy model should carry over to our world provided that we are careful."
A few years ago, a different research group that also included Harlow showed that holography works in quantum gravity in a similar way to how quantum error correction works in quantum computing. In the AdS/CFT correspondence, spacetime geometry in the anti-de Sitter Space emerges from quantum entanglement in the conformal field theory. Harlow and his colleagues showed that the emergent geometric data is, in fact, quantum error correcting codes, from a CFT standpoint.
The insight from this previous research was essential to prove the theorem in the researchers' recent study. In their new study, Ooguri and Harlow found that the way quantum error correction works is not compatible with any symmetry. Thus, once quantum mechanics and gravity are merged, no symmetry is exact.
"It has generally been believed that symmetry is a fundamental concept in nature," Ooguri said. "Many physicists believe that there must be a beautiful set of laws in nature, and that one way to quantify beauty is by symmetry. Some of the symmetry may be hidden in our world (or 'spontaneously broken," in physics terms), but they may manifest themselves if we look at nature at a more fundamental level. We showed that the belief expressed in the above is wrong. The laws of nature at the most fundamental level, where quantum mechanics and gravity is unified, have no global symmetry."
The study carried out by Ooguri and Harlow brings key insight to the physics field, ruling out the possibility of global symmetries in a wide class of quantum gravity theories. Their findings have implications for numerous areas of study, for instance predicting the instability of protons.
"Our findings predict that the proton should not be stable," Harlow said. "It isn't obvious, but it also predicts the existence of magnetic monopoles: isolated objects which carry magnetic charge. So far, we have never seen such an object, but people are still searching for them. Unfortunately, our results are not strong enough to say how many monopoles should exist, where they should be, or how long we have to wait to see a proton decay."
In their future work, Harlow and Ooguri would like to quantify how symmetry is broken. So far, they have merely proved that quantum gravity cannot have any symmetry without clarifying how it is taken apart. For instance, their findings suggest that the proton should decay, yet they do not clarify how it decays or how long it can live for before it does. These are very important questions, which the researchers hope to address in their future research.
"The Kavli Institute for the Physics and Mathematics of the Universe at the University of Tokyo, of which I am the director, is involved in the Hyper-Kamiokande project to be built in the Kamioka zinc mine in the central mountain area in Japan," Ooguri added. "One of the aims of the project is to see whether the proton decays and to do this experimenters will build a large water tank in the mine. According to our theorem, the protons should decay. But, we cannot tell experimenters how big the water tanks should be for them to be able to see the protons decay within a reasonable period of time. This is one example of why quantifying how symmetry is broken would be crucial. Daniel and I have some idea on how to quantify the way symmetry is broken and we are now continuing our investigation in this direction."
More information: Daniel Harlow et al. Constraints on Symmetries from Holography, Physical Review Letters (2019). DOI: 10.1103/PhysRevLett.122.191601
Daniel Harlow, Hirosi Ooguri. Symmetries in quantum field theory and quantum gravity. arXiv:1810.05338 [hep-th]. arxiv.org/abs/1810.05338
G. 't Hooft. Dimensional reduction in quantum gravity. arXiv:gr-qc/9310026. arxiv.org/abs/gr-qc/9310026
L. Susskind. The world as a hologram. arXiv:hep-th/9409089. arxiv.org/abs/hep-th/9409089
Juan M. Maldacena. The large N limit of superconformal field theories and supergravity. arXiv:hep-th/9711200. arxiv.org/abs/hep-th/9711200
Journal information: Physical Review Letters
© 2019 Science X Network