A leap into the continuum
Computing the dynamics of many interacting quantum particles accurately is a daunting task. There is however a promising calculation method for such systems: tensor networks, which are being researched in the theory division at the Max Planck Institute of Quantum Optics. The initial focus of tensor network was on quantum particles restricted to a lattice, just as they occur in crystals for example, or in the quantum registers of future quantum computers. In a new paper, the postdoctoral researcher Antoine Tilloy and the theory division director Ignacio Cirac managed to extend this approach to the continuum. A goal in the long run is an elegant calculation method for the quantum field theories that describes the basic forces of physics.
Describing the systems in which many quantum particles interact and collectively produce new phenomena is one the fundamental challenges of physics. One example of such a quantum many body phenomenon is superconductivity. The difficulty at hand is the particles influence each other. As a result, the quantum mechanical equations which describe this collective behavior can be derived, but not solved exactly.
In quantum mechanics, the dynamical equation must capture all the possible states the system potentially can be in. And there can be many. An example currently popular in physics are quantum bits. They are obtained for instance from specially prepared electrons or electrically charged atoms. Such qubits have two opposing states, which can take the values zero and one. But unlike a "classical" bit, the qubit can also be located in any superposition of those two states. If one now couples two qubits with a so-called quantum gate, the abstract mathematical space of all possible quantum states doubles. And every additional qubit doubles it again. Processors and data memories of conventional computers are literally overrun by this exponentially growing number of possible quantum states. Even supercomputers fail after more than a few dozen qubits. Only quantum computers, obeying the rules of quantum mechanics themselves, will one day be able to deal with the dynamics of larger quantum systems.
Making the incalculable calculable
The example of the qubits fits, because Ignacio Cirac and his colleagues are among the pioneers of this emerging field of quantum information technology. The method of "tensor networks," which is the subject of this paper, also originates from this field of research. It allows to cleverly reduce the gigantic space of all possible quantum states of a multi-particle system to a calculable size. "Imagine all possible quantum states of a many-particle system as a huge circular area," explains Antoine Tilloy. "But the states that are really relevant for our system fit within a much smaller circle." The art now is in finding this small circle in an abstract mathematical space, and that's what tensor networks can do.
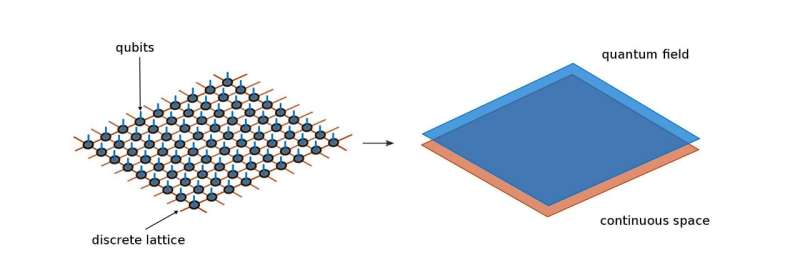
Tilloy is a postdoctoral researcher in Cirac's group and together they have just published an article on tensor networks in the journal Physical Review X. Originally, the physicists applied them to arrays of individual qubits. Tensor networks were thus initially relying on a grid of abstract mathematical objects—a bit like a mathematical string of pearls, living on discrete positions.
Tensor networks proved to be a successful tool to carry computations for a large class of quantum system confined to grids. This success gave theoretical research groups worldwide an idea: could this method also be applied to physical systems that do not live on grids, but rather in continuum space? In short, the answer is yes. In fact, the method of tensor networks can be extended to the continuum and this is what Tilloy and Cirac demonstrated in their new work.
New tool for quantum field theories
So-called quantum field theories could be an important field of application for this new toolbox. These theories form the foundation of today's physical worldview. They accurately describe how three of the four basic forces of physics function according to quantum mechanics. These forces are mediated by virtual particles that exist only for the short period of time needed to transmit their force.
In the electric force, for example, the mediating particles are virtual light quanta. "This falls under what is known as quantum electrodynamics and is well understood," says Tilloy. "Things get more complicated with what is known as quantum chromodynamics." QCD, as it is briefly called, describes the forces between the quarks, which in turn form the building blocks of the atomic nuclei, the protons and neutrons. Gluons, "adhesive particles," mediate the strongest force in physics. And this "glues" the quarks together.
But unlike the virtual photons, the gluons can also strongly influence each other. This "self-interaction" leads to the unpleasant fact that the equations of QCD can only be solved in borderline cases, at very high energy. For lower energies—the normal state of matter in our environment—this is not possible. For this reason, physicists so far have to work with approximate solutions. The standard step here is to break the continuum down into an artificial grid of points for which a powerful computer can then calculate approximate solutions.
"This step of discretization is complex," says Tilloy. In addition, such simplifications always have the disadvantage of breaking a fundamental symmetry of nature when dividing the continuum into a grid of discrete points. They are thus forced to move away from the actual physics. The method of continuous tensor networks could provide help here, because it does not require this prior discretization of space. Perhaps the behaviour of quarks and gluons at low energies will one day be understood. Today it's still an open problem, but the recently discovered continuous tensor networks might already be part of the solution.
More information: Antoine Tilloy et al. Continuous Tensor Network States for Quantum Fields, Physical Review X (2019). DOI: 10.1103/PhysRevX.9.021040
Journal information: Physical Review X
Provided by Max Planck Society