August 15, 2018 feature
Maze runners and square dancers: Cytosolic diffusion of nanosized objects in mammalian cells
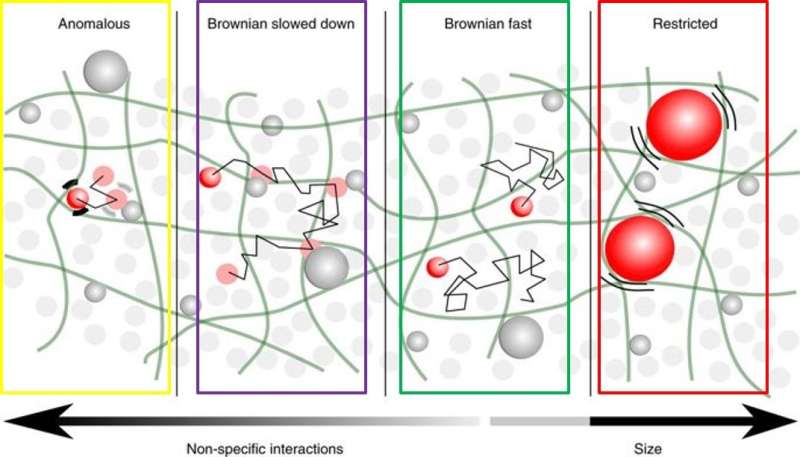
Cells are complex, multi-compartmentalized entities of matter enclosed with a variety of membrane-bound organelles ranging from the microscale (µm) down to the nanoscale (nm) in diameter. These structures intermingle in a crowded aqueous phase known as the cytoplasm, within which diffusion deviates from Brownian motion. Understanding the concept of "cell crowding" and the impact on intracellular mobility can enable controlled diffusion within cells for improved drug delivery and other medical applications. The eukaryotic cytoplasm is a biphasic poroelastic (fluid and solid interaction) medium, containing a fluid phase (cytosol with water and soluble proteins) and a solid phase (cytoskeleton and other organelles).
Experiments conducted with tracers on intracellular motion have typically revealed both Brownian and subdiffusive motion (or anomalous diffusion). High concentrations of macromolecules in the cytoplasm described as "obstructive molecular crowding" and biochemical interactions (electrostatic or hydrophobic) naturally affect the mobility of intracellular tracers.
As a result, a fundamental question has remained unresolved: Can a unified framework account for the large variability of behaviors observed in cytosolic diffusion? Now writing in Nature Materials, Fred Etoc and colleagues have used single-particle tracking of fluorescent nanoparticle (NP) tracers to observe and propose a unified framework that describes the diffusion dynamics of nanosized objects in the eukaryotic cell cytoplasm.
The researchers demonstrate:
- Inert objects were unaffected by obstructive molecular crowding to show Brownian motion, diffusing in a medium of low viscosity—if they were below approximately 75 nm in size. The researchers metaphorically compared them to "maze runners"
- Tracers that were approximately 25 nm in size but with increased non-specific interactions slowed down diffusion by three orders of magnitude, to gradually become anomalous and were compared to "square dancers"
The strength of non-specific interactions is captured into a single parameter using a simple continuous time random walk (CTRW) model, a textbook model that describes the random walk performed by diffusing particles. By fixing a few basic properties of the random walk, it was possible to observe that diffusing particles explored an area (mean square displacement – MSD) that grew linearly in time. To define the phenomenon of intracellular motion experimentally, Etoc and co-workers hijacked a cellular entry gate known as the pinocytosis pathway (observed with vesicle formation to transport biological materials), to import functionalized and fluorescently labelled nanoparticles (NPs) in to living HeLa cells. Cytoplasmic diffusion of individual NPs (20 to 50 NPs per cell) was recorded by time-lapse microscopy and quantified using single-particle tracking analysis.
A brief osmotic shock enabled the dispersion of NPs into the cytoplasm. The NP's diffusion-based exploration of the cell's interior was monitored by extensive single-particle tracking experiments. Using this approach, a variety of NP surface modifications and particle sizes ranging from 15 to 75 nm were observed to interact with the surroundings for pronounced diffusion anomalies.
In the study, Etoc et al. estimated mobility at short timescales by computing time averaged MSD at 60 ms, expressed in terms of the diffusion coefficient D60ms To represent the behavior of the whole population of NPs in each condition, the distribution of the parameters α (anomalous exponent) and D60ms arising from each individual trajectory, was presented as a two-dimensional (2-D) density map. Such density plots for hundreds of trajectories and conditions that integrated the results of α and D60ms were summarized elegantly in the findings.
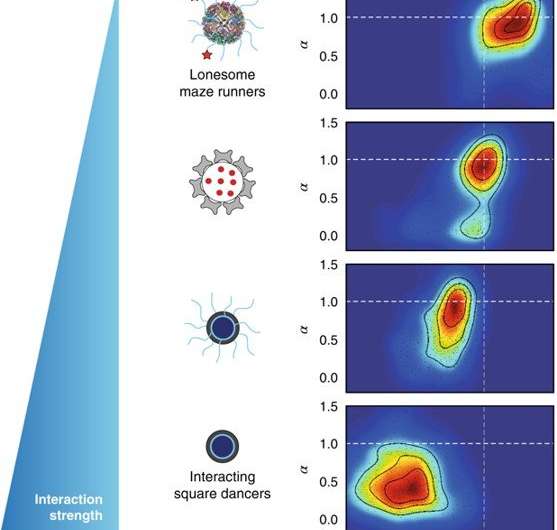
The experimental data were also explained with a minimal model based on continuous-time random walks, where particles were described to take power-law-distributed rests between periods of free diffusion motion. With this approach, the findings on MSD could be reproduced and captured as particle trajectories. Future work is required to explore if these results also apply to crowds of one to 10 nm-sized macromolecules in cells. Gaining an understanding of how anomalous random walks can be altered when modifying non-equilibrium conditions in cells (such as changed metabolic states) will keep both experimentalists and theorists busy.
Overall, the researchers proposed a unified framework to describe the dynamics of diffusion related to nanosized objects in the cell cytoplasm. The study also provided a quantitative benchmarking tool to design perfectly inert NPs that could diffuse within cells unhindered by obstacles, and defined them as "lone maze runners." Such insights may become crucial to design intracellular drug delivery pathways to easily reach molecular targets within cells in the future.
More information: Fred Etoc et al. Non-specific interactions govern cytosolic diffusion of nanosized objects in mammalian cells, Nature Materials (2018). DOI: 10.1038/s41563-018-0120-7
Matthias Weiss. A tale about square dancers and maze runners, Nature Materials (2018). DOI: 10.1038/s41563-018-0126-1
A. Einstein. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen, Annalen der Physik (2007). DOI: 10.1002/andp.19053220806
Alice B. Fulton. How crowded is the cytoplasm?, Cell (2004). DOI: 10.1016/0092-8674(82)90231-8
Felix Höfling et al. Anomalous transport in the crowded world of biological cells, Reports on Progress in Physics (2013). DOI: 10.1088/0034-4885/76/4/046602
O. Bénichou et al. Geometry-controlled kinetics, Nature Chemistry (2010). DOI: 10.1038/nchem.622
Journal information: Nature Materials , Cell , Reports on Progress in Physics , Nature Chemistry
© 2018 Phys.org