Study offers new theoretical approach to describing non-equilibrium phase transitions
Imaginary numbers are a solution to a very real problem in a study published today in Scientific Reports.
Two physicists at the U.S. Department of Energy's Argonne National Laboratory offered a way to mathematically describe a particular physics phenomenon called a phase transition in a system out of equilibrium. Such phenomena are central in physics, and understanding how they occur has been a long-held and vexing goal; their behavior and related effects are key to unlocking possibilities for new electronics and other next-generation technologies.
In physics, "equilibrium" refers to a state when an object is not in motion and has no energy flowing through it. As you might expect, most of our lives take place outside this state: we are constantly moving and causing other things to move.
"A rainstorm, this rotating fan, these systems are all out of equilibrium," said study co-author of the Valerii Vinokur, an Argonne Distinguished Fellow and member of the joint Argonne-University of Chicago Computation Institute. "When a system is in equilibrium, we know that it is always at its lowest possible energy configuration, but for non-equilibrium this fundamental principle does not work; and our ability to describe the physics of such systems is very limited."
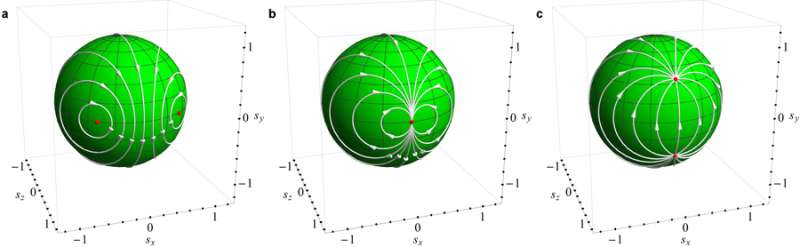
He and co-author Alexey Galda, a scientist with Argonne and the University of Chicago's James Franck Institute, had been working on ways to describe these systems, particularly those undergoing a phase transition - such as the moment during a thunderstorm when the charge difference between cloud and ground tips too high, and a lightning strike occurs.
They found their new approach to non-equilibrium physics in a new branch of quantum mechanics. In the language of quantum mechanics, the energy of a system is represented by what is called a Hamiltonian operator. Traditionally, quantum mechanics had held that the operator to represent the system cannot contain imaginary numbers if it would mean the energy does not come out as a "real" and positive value—because the system actually does exist in reality. This condition is called Hermiticity.
But physicists have been taking a harder look at operators that violate Hermiticity by using imaginary components, Vinokur said; several such operators discovered a few years ago are now widely used in quantum optics.
"We noticed that such operators are a beautiful mathematical tool to describe out-of-equilibrium processes," he said.
To describe the phase transition, Galda and Vinokur wrote out the Hamiltonian operator, introduced an applied force to take it out of equilibrium, and then they made the force imaginary.
"This is a trick which is illegal from any common-sense point of view; but we saw that this combination, energy plus imaginary force, perfectly mathematically describes the dynamics of the system with friction," Vinokur said.
They applied the trick to describe other out-of-equilibrium phase transitions, such as a dynamic Mott transition and a spin system, and saw the results agreed with either observed experiments or simulations.
In their latest work, they connected their description with an operation called a Möbius transformation, which appears in a branch of mathematics called topology. "We can understand non-equilibrium transitions now as topological transitions in the space of energy," Galda said.
This bit of quantum mischief needs to be understood more deeply, they said, but is valuable all the same; the theory describes basic areas of physics that are of great interest for next-generation electronics technology.
"For the moment the connection with topology looks like mathematical candy, a beautiful thing we can't yet use, but we know from history that if the math is elegant enough, very soon its practical implications follow," Vinokur said.
More information: Alexey Galda et al, Linear dynamics of classical spin as Möbius transformation, Scientific Reports (2017). DOI: 10.1038/s41598-017-01326-x
Journal information: Scientific Reports
Provided by Argonne National Laboratory