Researchers derive a unified topological speed limit for the evolution of physical states

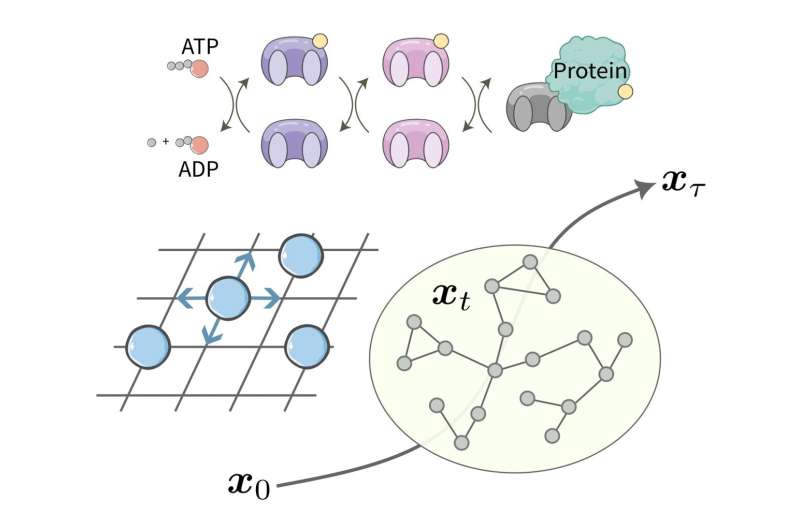
Physical systems evolve at a particular speed, which depends on various factors including the system's so-called topological structure (i.e., spatial properties that are preserved over time despite any physical changes that occur). Existing methods for determining the speed at which physical systems change over time, however, do not account for these structural properties.

Two researchers at Keio University in Japan have recently derived a speed limit for the evolution of physical states that also accounts for the topological structure of a system and of its underlying dynamics. This speed limit, outlined in a paper published in Physical Review Letters, could have numerous valuable applications for the study and development of different physical systems, including quantum technologies.

"Figuring out how fast a system state can change is a central topic in classical and quantum mechanics, which has attracted the great interest of scientists," Tan Van Vu and Keiji Saito, the researchers who carried out the study, told Phys.org. "Understanding the mechanism of controlling time is relevant to engineering fast devices such as quantum computers."

The notion that there is a limit in the operational time required for a system to shift from one physical state to another was first introduced several decades ago by Leonid Isaakovich Mandelstam and Igor Tamm. Since then, other research teams have explored this idea further, finding similar limits that can be applied to different types of physics systems.

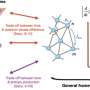
"These limits, called 'speed limits,' set ultimate rates at which a system can evolve to a distinguishable state and have found a variety of applications," Vu and Saito explained. "Nevertheless, conventional speed limits have the shortcoming of providing no meaningful bounds as the size of the system grows. One of the explanations is that the dynamics' topological nature, which arises from the network structure of underlying dynamics, has not been properly taken into consideration."

The key objective of the recent work by Vu and Saito was to devise a new speed limit that also considers the topological structure of a physical system and its underlying dynamics. This could ultimately help to set quantitative stringent bounds, potentially unveiling the physical mechanism underlying transformations from one state to another. Notably, this cannot be achieved using any of the speed limit methodologies introduced so far.

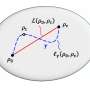
"Our idea is to employ a generalized version of the discrete Wasserstein distance to quantify the distance between the states," Vu and Saito said. "The Wasserstein distance originates from the idea of quantifying how many and how far a pile of goods must be carried to create another lump of goods from one lump. This distance, widely used in optimal transport theory, encodes topological information and can grow proportional to the size of the system."

To derive the unified topological speed limit, Vu and Saito mapped the time evolution of physical states to the optimal transport problem, exploiting the properties of the optimal transport distance. As part of their study, they also demonstrated the validity of their approach by applying it to chemical reaction networks and interacting many-body quantum systems.

"In our opinion, the most notable finding of our study is the discovery of the topological speed limit that yields accurate predictions for operational times and can apply to a wide range of dynamics," Vu and Saito said.

The new topological speed limit introduced by this team of researchers could ultimately be applied to research in various areas of physics, potentially improving the current understanding of different systems, in some cases facilitating their use for the development of new technologies. For instance, it enables the creation of a speed formula for chemical reactions, as well as setting universal constraints on the speed of bosonic transport and communication through spin systems.

"In the future, we plan to explore further applications of the derived topological speed limit from various directions," Vu and Saito added. "The utilization of the speed limit to better understand the underlying mechanisms of physical phenomena, such as the thermalization of closed and open systems, is a promising approach."

© 2023 Science X Network