June 3, 2016 report
Physicists discover an infinite number of quantum speed limits
(Phys.org)—In order to determine how fast quantum technologies can ultimately operate, physicists have established the concept of "quantum speed limits." Quantum speed limits impose limitations on how fast a quantum system can transition from one state to another, so that such a transition requires a minimum amount of time (typically on the order of nanoseconds). This means, for example, that a future quantum computer will not be able to perform computations faster than a certain time determined by these limits.
Although physicists have been investigating different quantum speed limits for different types of quantum systems, it has not been clear what the best way to do this is, or how many different quantum speed limits there are.
Now in a new paper published in Physical Review X, Diego Paiva Pires et al., from the UK and Brazil, have used techniques from information geometry to show that there are an infinite number of quantum speed limits. They also develop a way to determine which of these speed limits are the strictest, or in other words, which speed limits offer the tightest lower bounds. As the researchers explain, the search for the ultimate quantum speed limits is closely related to the very nature of time itself.
"In recent years, there has been an intense theoretical and experimental research activity to understand, on one hand, a fundamental concept in quantum mechanics such as time, and to devise, on the other hand, efficient schemes for the implementation of quantum technologies," coauthor Gerardo Adesso, at the University of Nottingham, told Phys.org. "A basic question that combines and underpins both areas of research is: 'How fast can a quantum system evolve in time?' Establishing general and tight quantum speed limits is crucial to assess how fast quantum technologies can ultimately be, and can accordingly guide in the design of more efficient protocols operating at or close to the ultimate bounds."
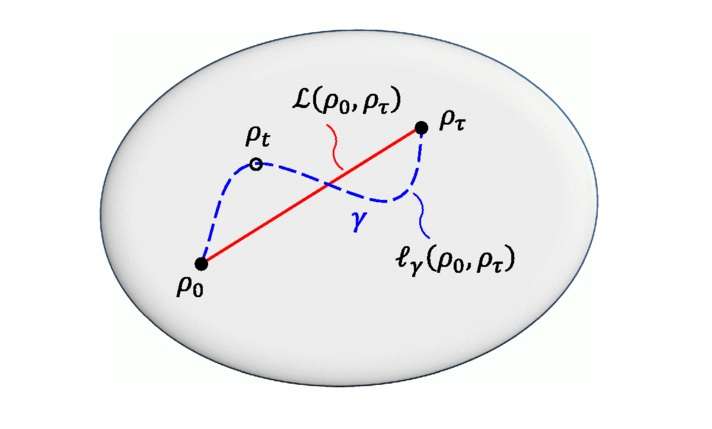
In order to determine how fast a quantum system can evolve from one state to another, it's necessary to be able to distinguish between the two states, and there are multiple ways to do this. In the new study, the physicists used a general method based on information geometry. From a geometric perspective, two distinguishable states can be represented by two points on the surface of some shape, such as a sphere or other manifold. Previous research has shown that there are an infinite number of corresponding metrics that can be used to measure the distinguishability of two quantum states.
In the new study, the physicists have shown that each of these metrics corresponds to a different quantum speed limit. The "strictest" quantum speed limit is determined by the metric that gives the shortest distance (also known as a 'geodesic') between the two points, or states, as measured along the manifold's curved surface.
"A different quantum speed limit arises from each of these metrics in such a way that the tightest bound for a given dynamics is specified by the metric whose geodesic is best tailored to the given dynamical path," explained coauthor Marco Cianciaruso, also at Nottingham.
Overall, the new approach unifies most of the previous results by interpreting them under a single, new framework. On one hand, the researchers could derive the tightest bounds to date on quantum speed limits for some relevant instances, such as quantum bits undergoing dissipative and decohering evolutions. On the other hand, they could also show that bounds that have been previously proposed for other instances are truly the optimal bounds—no tighter bounds will ever be found.
In the future, the researchers plan to experimentally investigate the quantum speed limits derived here using nuclear magnetic resonance (NMR) techniques.
"Our findings are expected to have an impact on the fields of quantum information, computation, simulation, and metrology," said Diogo Soares-Pinto at the Sao Carlos Institute of Physics, who supervised the project.
More information: Diego Paiva Pires et al. "Generalized Geometric Quantum Speed Limits." Physical Review X. DOI: 10.1103/PhysRevX.6.021031
Journal information: Physical Review X
© 2016 Phys.org