Mathematician calculates wave velocity for post-stroke therapy
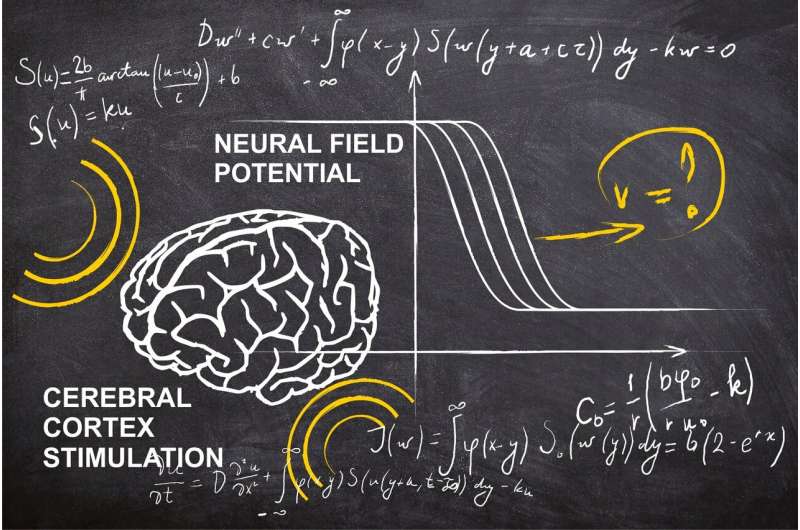
A RUDN mathematician calculated the velocity of wave propagation in the brain in the course of external stimulation. This procedure is used to treat stroke patients. To do so, the scientists generally formulated the task by creating a reaction-diffusion equation and carried out a theoretical study of it. The results of the study were published in Applied Mathematics Letters.
Many biological and chemical processes can be described with so-called reaction-diffusion equations. Usually, tasks of this type occur in biologically distributed systems, i.e. structures in which a certain biological parameter is unevenly distributed in space. Such systems include the nerve tissue. Energy transfer processes help to consider such systems as a whole. They are described by diffusion components of a reaction-diffusion equation. Due to this connection between points in space, so-called excitation waves (e.g. a nerve impulse) can propagate in such media.
In some cases, the velocity and shape of an excitation wave can be calculated using existing mathematical methods. However, they are not applicable to excitation waves in the cerebral cortex. A RUDN mathematician together with his Russian and foreign colleagues solved this problem in general terms.
The authors considered an integrodifferential equation, i.e. an equation containing both integrals and derivatives. Besides the function in question, the equation contained additional parameters that accounted for the cohesiveness of the medium, its response, and its density from the mathematical point of view. These parameters could also be interpreted from the point of view of physics—in this case, they described the excitation of neurons, their interconnection, and the speed at which a nerve impulse faded. Besides the equation itself, the mathematicians set out boundary conditions causing a progressive wave in the equation when met.
Progressive wave propagation speed is one of the most important parameters in reaction-diffusion systems. However, it is impossible to find it in an explicit way for external brain stimulation. A RUDN mathematician managed to obtain its minimax representation. This method can analyze a parameter's upper and lower limits.
Theoretical results obtained by the mathematicians have already been applied to the calculation of post-stroke brain stimulation parameters. The properties of nerve tissues as a distributed biological medium change when neurons are damaged by a stroke. In particular, the excitation of neurons changes, and their interconnection deteriorates, slowing down the propagation of a progressive wave (nerve impulse). However, it may be restored using external stimulation. To do so, electrodes are implanted into the brain, or an external magnetic field generating electromagnetic impulses is created. This procedure is well-known and is already in use. However, until now it has been impossible to make the exact calculation of optimal external impulse parameters.
"Our method of minimax evaluation of progressive wave propagation may be used to calculate the speed of a nerve impulse in undamaged areas of the cerebral cortex. Based on the obtained values, one can select external stimulation parameters tailored to each patient's needs and restore the nerve impulse speed in damaged tissues," said Vitaly Volpert, the author of the article, and the head of the laboratory of mathematical modeling in biomedicine at RUDN.
More information: N. Bessonov et al. Estimate of the travelling wave speed for an integro-differential equation, Applied Mathematics Letters (2018). DOI: 10.1016/j.aml.2018.07.037
Provided by RUDN University