May 30, 2024 feature
This article has been reviewed according to Science X's editorial process and policies. Editors have highlighted the following attributes while ensuring the content's credibility:
fact-checked
peer-reviewed publication
trusted source
proofread
A surprising result for a group's optimal path to cooperation
What is the best way for a group of individuals to cooperate? This is a longstanding question with roots in game theory, a branch of science which uses mathematical models of how individuals should best strategize for the optimal result.
A simple example is the prisoner's dilemma: Two people are arrested for an alleged bank robbery. The police take them downtown and place them in individual, isolated interrogation rooms.
The police admit they don't have enough evidence to convict them both, and give each the same option: if he confesses and his partner does not, they will release the confessor and convict the other of the serious charge of bank robbery. But if one does not confess and the other does, the first will get a lengthy prison sentence and the other will be released. If both confess, they will both be put away for many years. If neither confesses, they will be arraigned on a lesser charge of gun possession.
What should each do to minimize their time in jail? Does an individual stay silent, trusting his partner to do the same and accept a shorter prison sentence? Or does he confess, hoping the other stays silent. But what if the other confesses too? It is an unenviable position.
There is no correct solution to the prisoner's dilemma. Other similar problems are the game of chicken, where each driver races towards the other, risking a head-on crash, or swerving away at the last minute and risking humiliation—being called "chicken" for a lack of courage. Many other simple games exist.
Now imagine a group—they may be people, or they may be cellular organisms of some sort. What kind of cooperation gives the optimal result, when each individual is connected to some others and pays a cost (money, energy, time) to create a result that benefits all? It's a given that individuals are selfish and act in their own best interests, but we also know that cooperation can result in a better outcome for all. Will any take the risk, or look out only for themselves?
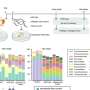
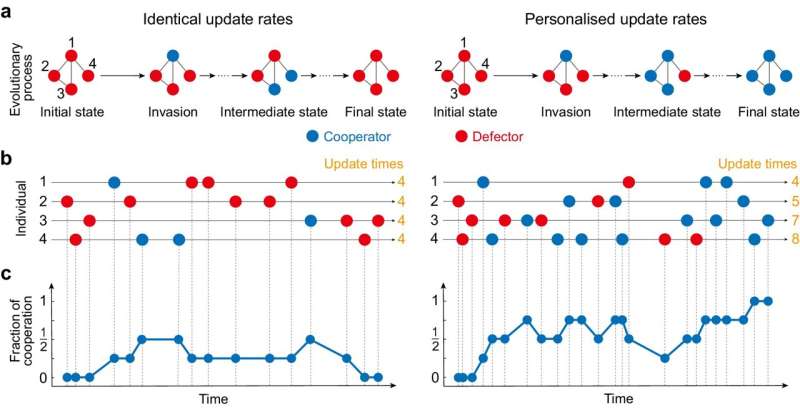
A long-standing result is that, in a homogeneous network where all individuals have the same number of neighbors, cooperation is favored if the ratio between the benefit provided by a cooperator and their associated cost paid exceeds the average number of neighbors.

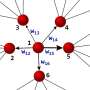
But people are not homogeneous, they're heterogeneous, and they don't usually have the same number of links to neighbors as does everyone else or change their strategy at the same rates.
It is also known that allowing each individual to update their strategy at exactly the same time, such as immediately mimicking their neighbor, significantly alters the evolution of cooperation. Previous investigations have reported that pervasive heterogeneous individual connections hinder cooperation when it's assumed that individuals update their strategies at identical rates.
Now a group of researchers located in China, Canada and the US have found a surprising result: when individuals' strategy update rates vary inversely with their number of connections, heterogeneous connections outperform homogeneous ones in promoting cooperation. The study is published in the journal Nature Communications.
"How to analyze the quantitative impact of the prevalent heterogeneous network structures on the emergence of group optimal strategies is a long-standing open question that has attracted much attention," said Aming Li, a co-author and Assistant Professor in Dynamics and Control at Peking University.
Li's team solved the problem by analytical calculations backed up by computer simulations, to find the fundamental rule for maintaining collective cooperation: "The nodes with substantial connections within the complex system should update their strategies infrequently," he says. That is, individual strategy update rates should vary inversely with the number of connections they have in the network. In this way, a network with heterogeneous connections between individuals outperforms a network with homogeneous connections in promoting cooperation.
The team has also developed an algorithm that most efficiently finds the optimal strategy update rates that brings about the group's optimal strategies, which they call OptUpRat. This algorithm helps collective utility in groups and, Li says, "is also essential in developing robotic collaborative systems." The finding will be useful to researchers in such multidisciplinary fields as cybernetics, artificial intelligence, systems science, game theory and network science.
"We believe that utilizing AI-related techniques to optimize individual decisions and drive collective intelligence will be the next research hotspot."
More information: Yao Meng et al, Dynamics of collective cooperation under personalised strategy updates, Nature Communications (2024). DOI: 10.1038/s41467-024-47380-8
Journal information: Nature Communications
© 2024 Science X Network