June 20, 2024 feature
This article has been reviewed according to Science X's editorial process and policies. Editors have highlighted the following attributes while ensuring the content's credibility:
fact-checked
peer-reviewed publication
trusted source
proofread
High-temperature superconductivity: Exploring quadratic electron-phonon coupling
A new study published in Physical Review Letters (PRL) explores the potential of quadratic electron-phonon coupling to enhance superconductivity through the formation of quantum bipolarons.
Electron-phonon coupling is the interaction between electrons and vibrations in a lattice called phonons. This interaction is crucial for superconductivity (resistance-free electrical conductance) in certain materials as it facilitates the formation of Cooper pairs.
Cooper pairs are pairs of electrons bound together via attractive interactions. When these Cooper pairs condense into a coherent state, we get superconducting properties.
Electron-phonon coupling can be categorized based on its dependence on phonon displacement, which means how much the lattice vibrates. The most commonly considered case is when electron density linearly couples to lattice displacements, causing a lattice distortion to surround every electron.
The researchers wanted to study if superconductivity can be enhanced for materials exhibiting quadratic coupling, which is when the interaction energy is proportional to the square of the phonon displacement.
Phys.org spoke to the co-authors of the study, Zhaoyu Han, a Ph.D. candidate at Stanford University and Dr. Pavel Volkov, Assistant Professor at the Department of Physics, University of Connecticut.
Speaking of his motivation behind pursuing this research, Han said, "It has been one of my dreams to identify and propose new mechanisms that may help achieve high-temperature superconductivity."
Dr. Volkov said, "The superconductivity of doped strontium titanate was discovered more than 50 years ago, however, its mechanism remains an open question, with conventional mechanisms being unlikely. This is why I started looking into alternative electron-phonon coupling mechanisms."
Linear coupling and its challenges for superconductivity
As mentioned earlier, coupling can be categorized as linear or quadratic coupling.
Linear coupling refers to the scenario when the coupling is proportional to the displacement of the phonons. On the other hand, quadratic coupling depends on the square of phonon displacement.
They can be identified by studying the symmetry of the material, experimental observations, and theoretical frameworks. Their implications for superconductivity, however, appear quite different.
Linear coupling, seen in most superconducting materials, is extensively studied because of its prevalence in many materials and has a theoretical framework.
However, conventional superconductors with linear electron-phonon coupling face limitations. These materials have a low critical temperature, which is the temperature below which the material can exhibit superconductivity.
Han explained, "The critical temperatures for these superconductors are usually below 30 Kelvin or -243.15 degrees Celsius. This is partly because the Cooper pair binding energy and the kinetic energy are exponentially suppressed in the weak and strong coupling regimes, respectively."
In weak coupling, the electron-phonon interactions are weak due to the low binding energy. In strong coupling, the interactions are stronger, leading to a higher effective mass of the Cooper pairs, suppressing superconductivity.
However, the suppression hinders any efforts to improve the critical temperatures in such materials by just increasing the coupling strength, encouraging the researchers to explore materials with quadratic electron-phonon coupling, which are not as well understood.
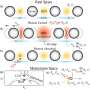
Holstein model and quantum bipolarons
The Holstein model is a theoretical framework used to describe the interaction between electrons and phonons. It has previously been used to study the generic physics of linear electron-phonon coupling.
The researchers extended the Holstein model to incorporate quadratic electron-phonon coupling in their study.
The Holstein model helps calculate quantities such as the binding energy of Cooper pairs and the critical temperature of superconductors.
In conventional materials, the binding of electrons mediated by phonons leads to the formation of Cooper pairs.
The interaction is linear, meaning that the strength of the coupling increases with the amplitude of lattice vibrations. This interaction can be understood using classical physics principles and is well-supported by experimental observations like isotope effects.
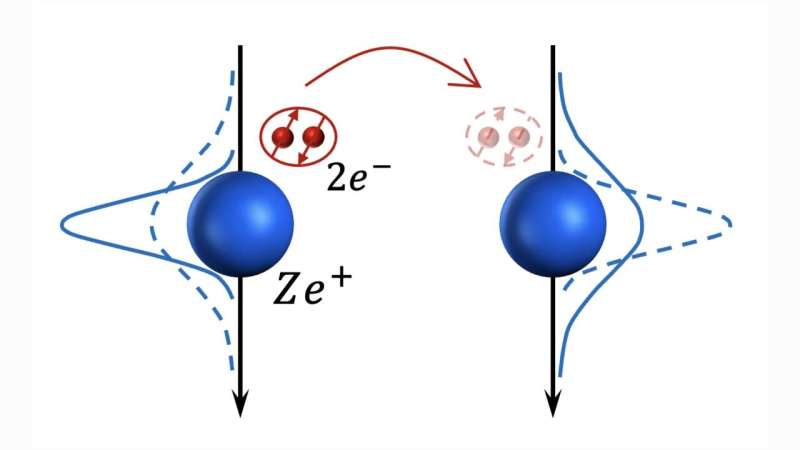
In the case of quadratic coupling, this is totally different. By extending the Holstein model to incorporate the second-order dependence of the coupling on phonon displacement, the researchers account for quantum fluctuations (random motion) of phonons and zero-point energy (the energy of phonons at 0 Kelvin).
The electrons interact with the quantum fluctuations of phonons, forming "quantum bipolarons." Unlike linear coupling, the origin of the attractive interactions is purely quantum mechanical.
Superconductivity in weak and strong coupling limit
The researchers found that when the electron-phonon interaction is weak, the mechanism by which electrons pair up to form Cooper pairs is not effective, similar to the linear case. This leads to a low critical temperature which can be affected by the mass of the ions (isotope effect), but in a different way than in the linear case.
In other words, the material's (low) critical temperature can change significantly with different atomic masses.
In contrast, when the electron-phonon interactions are strong, we get the formation of quantum bipolarons, which can become superconducting at a temperature set by their effective mass and density.
Below the critical temperature, the condensate of quantum bipolarons can move freely without disturbing the crystal. More mobility leads to a superconducting state, which is more stable and has a higher critical temperature. Unlike the linear mechanism, the quantum bipolaron mass is only mildly enhanced with coupling, allowing for higher critical temperatures.
"Our work demonstrates that this mechanism allows for higher transition temperatures, at least for strong coupling. What's also good is that this mechanism does not require any special preconditions to be operative, and there are quite realistic conditions where it will be dominant," explained Dr. Volkov.
Han predicted, "Based on fundamental physical constants relevant for solid materials, an optimistic estimation of the critical temperature achievable by this mechanism can be of the order of 100 Kelvin."
Future work
"The potential implication, first and foremost, would be an enhancement of superconducting transition temperature. Superconductivity also sensitively depends on the properties of electrons; so, to achieve strong coupling we propose using specifically engineered superlattices for electrons," explained Dr. Volkov.
The researchers mention that theoretically, the next step would be to find the optimal regime of coupling strength for superconductivity. The researchers also hope that experimentalists will explore superlattice materials with large quadratic electron-phonon couplings.
"Experimentally, creating superlattices via patterning or using interfaces between twisted materials could be a promising path to realize the type of superconductivity we predicted," said Dr. Volkov.
Han also pointed out, "It is crucial to identify materials with large quadratic electron phonon couplings from ab initio calculations, since this has not been systematically explored."
More information: Zhaoyu Han et al, Quantum Bipolaron Superconductivity from Quadratic Electron-Phonon Coupling, Physical Review Letters (2024). DOI: 10.1103/PhysRevLett.132.226001. On arXiv: DOI: 10.48550/arxiv.2312.03844
Journal information: Physical Review Letters , arXiv
© 2024 Science X Network