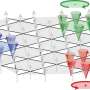
Russian and German physicists developed a mathematical model of trapped atoms and ions

A team of physicists from RUDN, JINR (Dubna), and the University of Hamburg (Germany) developed a mathematical model for describing physical processes in hybrid systems that consists of atoms and ions cooled down to temperatures close to absolute zero. Such atom-ionic systems might serve as a basis for the elements of the quantum computer—a device operating on quantum phenomena and exceeding regular computers by calculation speed. Right now, this is just a hypothetical concept, but the new development could make it reality sooner. The results of the study were presented at the 22nd International Conference on Few-Body Systems in Physics that took place in Caen (France) in July 9-13.
It is difficult to study processes at the level of individual atoms and ions at room temperature due to their thermal motion, which causes disturbances that lead to considerable inaccuracy of measurements. The main cause of observation errors is the Doppler effect. However, if the atoms are cooled down, reducing the speed of their thermal motion, this effect can be suppressed.
Atoms can be cooled using a laser, but it's important to select the proper frequency and direction. The same laser can create a so-called trap for cooled atoms—a standing light wave (i.e. a wave that does not move but fluctuates in one place) keeps the atoms fixed in a confined region of space. This trap can be compared to an egg case that prevents the eggs from moving around. Such a trap can be used as a model system for studying quantum processes including solid state physics and high energy physics. However, it is quite difficult to give a detailed mathematical description of systems of trapped quantum particles.
"The two-body problem (e.g. a hydrogen atom or two colliding atoms) is the basis of quantum mechanics. Each body has three coordinates (X, Y, and Z). In free space, this problem may be reduced to relative motion of two particles by separation of their center-of-mass. The number of variables left in the problem is now three instead of six. The absence of a preferred direction helps reduce this problem to an even simpler one-dimensional radial equation (i.e. an equation with one variable) by separation of angular variables. But when two quantum particles are trapped, an additional condition appears, which is preferential direction. In this case, the problem cannot be reduced to a one-dimensional equation. It becomes two-dimensional if the atoms are identical and six-dimensional if they are distinguishable or if an atom-ionic system is considered. Many scientists are able to solve two-dimensional equations, but three-dimensional ones are already quite a complicated problem for modern numerical mathematics. This is the area where new methods have to be developed," said Vladimir Melezhik, the author of the study.
Together with physicists from the University of Hamburg, Melezhik developed a mathematical method reducing multi-dimensional calculations to a system of one-dimensional equations to simplify and speed up the calculations. The authors used it to describe atomic systems with different parameters (intensity of effective interparticle interaction, initial state population, and particle energy). The method also proved applicable to hybrid atom-ionic systems. If ions are trapped, new complex quantum effects can be studied. The developed algorithm provides for the calculation of collisions of atoms and ions to each other and the laser trap. In the future, such hybrid structures can potentially help to model the elements of quantum computers.
More information:
The author acknowledges the support by the Russian Foundation for Basic Research, Grant No. 18-02-00673.
22nd International Conference on Few-Body Systems in Physics: web.infn.it/eu-few-body/
Abstracts: fb22-caen.sciencesconf.org/dat … ook_fb22_caen_en.pdf
Provided by RUDN University