July 20, 2018 feature
A phonon laser operating at an exceptional point
The basic quanta of light (photon) and sound (phonon) are bosonic particles that largely obey similar rules and are in general very good analogs of one another. Physicists have explored this analogy in recent experimental investigations of a phonon laser to provide insights into a long-debated issue of how a laser—or more specifically, its line width—is affected when operated at an exceptional point (EP). Exceptional points are singularities in the energy functions of a physical system at which two light modes coalesce (combine into one mode) to produce unusual effects. Until recently, the concept mainly existed only in theory, but received renewed attention with experimental demonstrations in optical systems such as lasers and photonic structures. The experimental studies involved systems with parity-time symmetry for balanced gain and loss of material, to ensure robust light intensity, immune to backscatter. While closed and lossless physical systems are described by Hermitian operators in quantum physics, systems with open boundaries that exhibit exceptional points (EPs) are non-Hermitian.
Experimental studies of the EP mostly concern such parity-time symmetric systems that cleverly exploit the interplay between gain and loss to enable entirely new and unexpected features. In one such conceptual leap, unusual optical effects produced in these systems rendered the medium invisible in one direction, a step toward next-generation optical materials with unique properties not seen with natural materials. Such concepts have initiated intense research efforts to explore non-Hermitian systems both experimentally and theoretically.
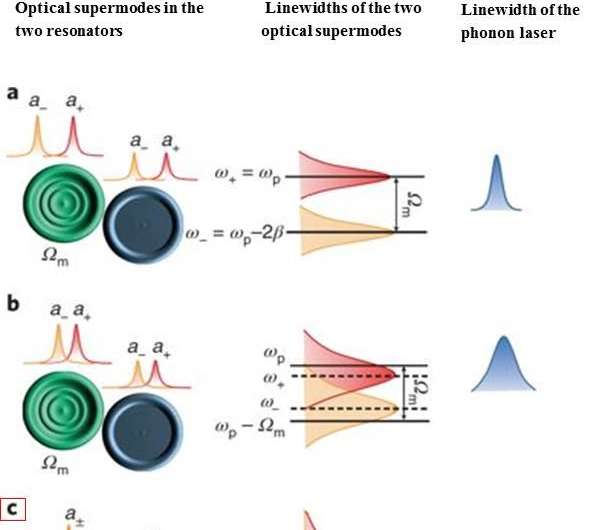
Before the first laser was experimentally demonstrated, Schawlow and Townes calculated the fundamental quantum limit for its linewidth; EPs are historically associated with extreme broadening of the laser linewidth—beyond the fundamental Schawlow–Townes limit. Although theoretical models have provided a framework to calculate laser linewidth, they fail to resolve the problem directly at the EP. Experimentally, it is not straightforward to steer a laser directly to an EP, since photonic laser modes become unstable close to an EP, causing chaotic lasing that could be erroneously perceived as an extremely broad laser line.
What really happens to the linewidth when a laser operates at an EP in practice has therefore remained unclear up until now. Understanding the mechanisms responsible for linewidth broadening will enable laser resources with new capabilities that we did not have access to before. Zhang et al., provide an elegant new strategy to tackle this problem as published in Nature Photonics, by working with a phonon laser rather than its optical (photonic) counterpart, to observe its operation at an exceptional point.
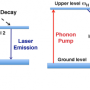
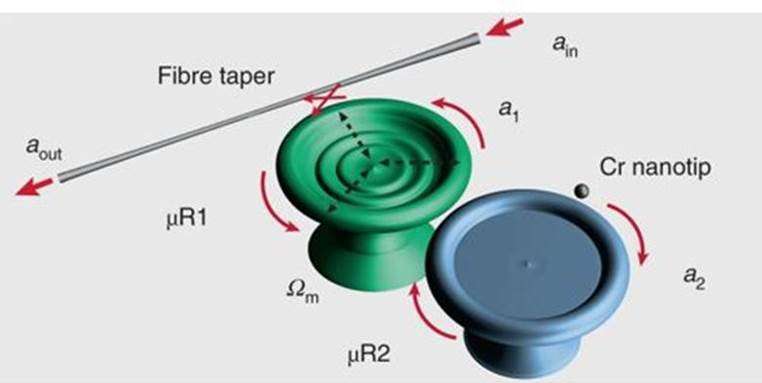
In the study, phonon lasers produce coherent sound oscillations (mechanical vibrations) induced by optical pumping, a concept previously developed by Grudinin, Vahala and co-workers ,with characteristics typical for photon lasers. In the present experiment, the researchers used a similar optomechanical system with two coupled silica whispering-gallery-mode microresonators (green and blue). The compound phonon-laser system was steered toward or away from its EP to observe the behavior of phonon lasing near an EP.
To observe linewidth broadening, the physicists optically excited the mechanical mode of the experimental device with light from a tunable laser coupled to a single microresonator (green) by means of a tapered fiber. Then, to steer the system toward or away from its EP, they introduced additional loss to the second microresonator (blue) using a chromium-coated silica nanofibre tip.
The interplay between gain and loss was exploited in this way to tune a phonon laser to an EP. Phonon lasing is interpreted as a three-wave parametric process in which two waves are optical and the third wave is acoustic or mechanical. Zhang et al. provided direct experimental evidence to show complete overlap of optical supermodes at EP, and that EP-enhanced optical noise can be transferred directly to mechanical noise, leading to the observed linewidth broadening in phonon lasers.
The practical benefits are easy to grasp: Sound waves propagate at a speed that is about five orders of magnitude less than the speed of light, and the wavelength of sound is thus correspondingly shorter than that of light of the same frequency. This feature can enable highly precise, nondestructive measurements and imaging, as well as achieve a high concentration of energy with focused sound waves. The present work opens new perspectives for the relationship between noise and non-Hermitian physics, with potential applications in related fields such as signal processing technologies. The system can be used as an on-chip phononic device analogous to fully integrated photonic devices for information processing. More interestingly, the studied platform can broaden insights in non-Hermitian physics by enabling the detection and control of EPs in two-level or multi-level systems.
More information: Jing Zhang et al. A phonon laser operating at an exceptional point, Nature Photonics (2018). DOI: 10.1038/s41566-018-0213-5
Ramy El-Ganainy et al. Non-Hermitian physics and PT symmetry, Nature Physics (2018). DOI: 10.1038/nphys4323
Jacob Khurgin. Phonon lasers gain a sound foundation, Physics (2010). DOI: 10.1103/Physics.3.16
Bo Zhen et al. Spawning rings of exceptional points out of Dirac cones, Nature (2015). DOI: 10.1038/nature14889
Alois Regensburger et al. Parity–time synthetic photonic lattices, Nature (2012). DOI: 10.1038/nature11298
Aram Mooradian. Laser Linewidth, Physics Today (2008). DOI: 10.1063/1.880973
Turning loss into gain. Nature Photonics doi.org/10.1038/s41566-017-0067-2
Interview by David F. P. Pile. Gaining with loss, Nature Photonics (2017). DOI: 10.1038/s41566-017-0060-9
H. Hodaei et al. Dark-state lasers: mode management using exceptional points, Optics Letters (2016). DOI: 10.1364/OL.41.003049
Journal information: Nature Photonics , Nature , Nature Physics , Physics Today , Optics Letters
© 2018 Phys.org