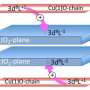
Intertwining of superconductivity and magnetism
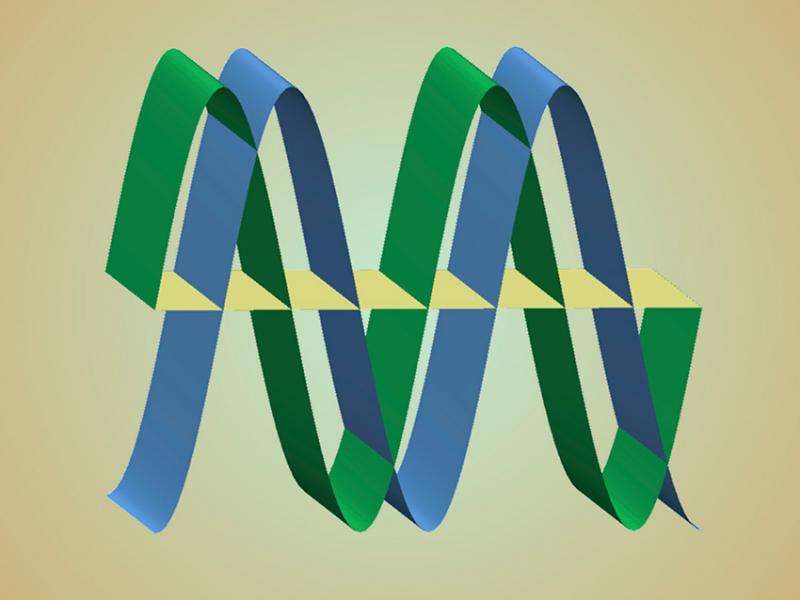
Inelastic neutron scattering experiments on a copper-oxide superconductor reveal nearly static, spatially modulated magnetism. Because static magnetism and superconductivity do not like to coexist in the same material, the superconducting wave function is also likely modulated in space and phase-shifted to minimize overlap, consistent with recent theory.
The new insight regarding the coexistence of superconductivity and atomic magnetism will aid in the development of a predictive theory for high-temperature superconductivity, one that can assist in the design and discovery of new superconductors with improved properties.
The observation of coexisting magnetism and superconductivity in a particular copper-oxide superconductor suggests that the two types of order can be spatially modulated and intertwined, supporting recent theoretical predictions. Understanding the relationship between superconductivity and a type of atomic magnetic correlation (antiferromagnetism, wherein neighboring atomic spins are oriented in opposite directions) remains a challenge. The magnetism is associated with the localization of electrons, whereas superconductivity is a state in which electrons are paired and can flow without resistance.
Previous experiments have shown that these two states do not like to coexist in the same space. Researchers from Brookhaven National Laboratory characterized slow magnetic fluctuations in a copper-oxide superconductor. Their discovery shows that the slowly fluctuating magnetism does not disappear in the superconducting state; in fact, it grows stronger at the lowest fluctuation frequencies.
The state of intertwined superconductivity and antiferromagnetism that has been proposed by theorists provides a likely explanation of the observations. These results indicate an intimate connection between superconductivity and magnetism in copper oxides, an important clue for developing a predictive theory of high-temperature superconductivity.
More information: "Neutron-scattering evidence for a periodically modulated superconducting phase in the underdoped cuprate La1.905Ba0.095CuO4," Physical Review Letters 113, 177002, 2014. DOI: 10.1103/PhysRevLett.113.177002
Journal information: Physical Review Letters
Provided by US Department of Energy