August 26, 2013 report
Physicists suggest electrical networks more at risk of cascading failure than thought
(Phys.org) —A team of physicists from Israel and the U.S. has discovered that mathematical modeling suggests modern electrical networks may be more vulnerable to cascading collapse than has been previously thought. In their paper published in the journal Nature Physics, the researchers found that previous models that showed such networks to be robust were based on more randomness than is typically found in real-world networks such as the Internet and electrical systems.
Modern electrical networks such as those used in the United States have demonstrated a vulnerability to cascading collapse—most famously by the widespread outage that occurred a decade ago taking out power to millions in the northeast and Midwest parts of the country (and parts of Canada). That outage was traced to a series of mistakes that occurred after a software bug caused problems in an alarm system (following some tress falling on power lines) in a single control room. After one small part of the network went down, other parts soon followed, resulting in the largest blackout in U.S. history. Utility representatives insist that technological advances and improvements to the infrastructure have been made which have resulted in a network that is today very unlikely to experience such an outage again. In this new effort, the physicists disagree.
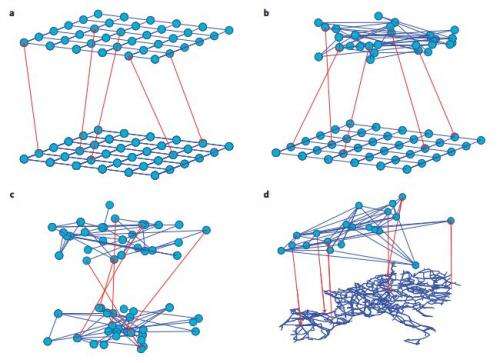
The problem with mathematical models that are used to demonstrate how a network might continue working when failures occur, or when they don't, the team writes, is that they are used to describe networks with nodes randomly spaced. The Internet, they note, and electrical systems are not randomly spaced because of population density differences, geography, etc.—taking out randomness results in orderly lattices that lead to more critical nodes. That in turn, of course, leads to less stable networks.
A mathematical model can't fully describe a real-world electrical grid, of course, and it's entirely possible that components have been put in place that are able to counteract the lack of randomness in the system currently in use. On the other hand, it's also possible that such measures have vulnerabilities as well. The researchers suggest utilities add long lines to connect critical nodes to bring the system as a whole back to a more random state to make it more robust.
More information: The extreme vulnerability of interdependent spatially embedded networks, Nature Physics (2013) DOI: 10.1038/nphys2727
Abstract
Recent studies show that in interdependent networks a very small failure in one network may lead to catastrophic consequences. Above a critical fraction of interdependent nodes, even a single node failure can invoke cascading failures that may abruptly fragment the system, whereas below this critical dependency a failure of a few nodes leads only to a small amount of damage to the system. So far, research has focused on interdependent random networks without space limitations. However, many real systems, such as power grids and the Internet, are not random but are spatially embedded. Here we analytically and numerically study the stability of interdependent spatially embedded networks modelled as lattice networks. Surprisingly, we find that in lattice systems, in contrast to non-embedded systems, there is no critical dependency and any small fraction of interdependent nodes leads to an abrupt collapse. We show that this extreme vulnerability of very weakly coupled lattices is a consequence of the critical exponent describing the percolation transition of a single lattice.
Journal information: Nature Physics
© 2013 Phys.org