From black hole entropy to the complexity of plant leaves: An intriguing linkage

Complexity of biological forms has fascinated humankind over the years. Different species of plants have different leaf shapes. Have you ever wondered why it is so? Why does this shape diversity exist? Plants can change their leaf shapes over time and space. But how?

Does the distinct shape of leaf forms play a significant role in energy optimization? In fact, the shape of leaves has a lot to do with adapting to their surrounding environment. How is the unfolding of shape related to the evolutionary process of nature? These intriguing questions have led us to focus on quantitative approaches to the complexity of plant leaves.

Quantifying leaf shapes using Euclidean shapes, such as circles, triangles, etc., are appropriate to only a few plant species. Therefore, various quantitative measures of leaf shapes have been developed with varying accuracy. But Is the shape of an object really its actual shape? Visual perception of definite shape or geometry of physical objects is only an abstraction.

Digging deep into the subsistence of shape reveals that the patterns or boundaries we see are not perfect. The shape and boundary of any physical object are just a perception rendered by human vision. A realistic boundary will change with magnification and can be perceived as diffuse microscale interfaces with finite thickness.

How are leaf geometry and black hole entropy linked?

In 1972, physicist Jacob Bekenstein devised a nifty formula for calculating a black hole's entropy. The entropy formulation is known as the Bekenstein-Hawking entropy and is proportional to the area of the black hole event horizon. It is one of the few prominent examples relating geometry to entropy.

Later, in 2008, the structure of the Bekenstein-Hawking entropy formula was formulated by scientist Georg J. Schmitz using geometric considerations of a geometric sphere based on a continuous 3D extension of the Heaviside function, which draws on the phase-field concept of diffuse interfaces.

We followed multidisciplinary approaches to quantify the leaf complexity. We derived the complexity of plant leaves as geometry entropy from an information point of view by adopting the notion of Bekenstein-Hawking formulation of black hole entropy by Georg J. Schmitz. Our results are published in the journal PLOS ONE.

While the perceived geometry at an object's sharp interface (macro) creates a Euclidean illusion of actual shape, the notion of diffuse interfaces (micro) allows an understanding of the realistic form of objects. We perceived the leaf's boundary as a narrow leaf-environment diffuse interface, which we consider analogous to the diffuse interface in phase-field theory.

By utilizing the concept of mereotopology, a less well-known discipline in the scientific world that connects the static relationship between objects by logical expressions, true or false, we ultimately derived the geometry entropy for a geometric circle, which is then transformed for the geometric entropy of plant leaves.

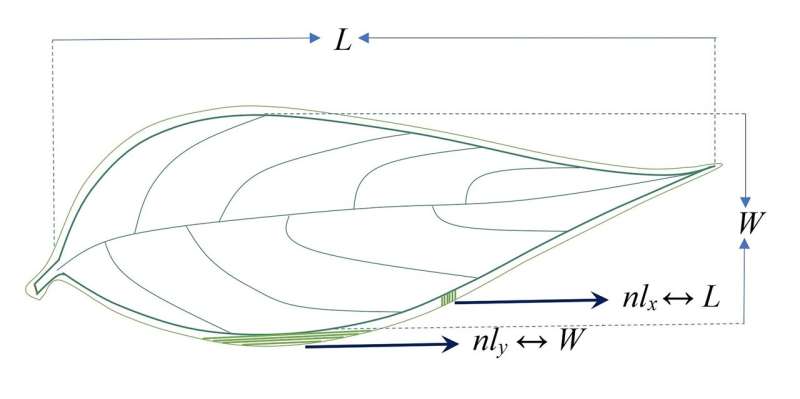
Our approach was purely theoretical and based on a continuous 2D extension of the Heaviside function and phase-field functions on a narrow leaf-environment diffuse interface. Description of the shape of the leaf-environment diffuse interface was achieved by the statistical distribution of gradients in the diffuse interface. The geometric entropy expression is proportional to the leaf perimeter and square root of the leaf area and matches with the well-known leaf dissection index.

What are the potential applications of geometric entropy?

Geometric entropy is an inherent complexity measure that outperforms other complex geometric morphometrics. It is free from time-consuming pre-processing techniques and posits a prospective method to quantify the extent of variation in leaf shapes, such as deep lobiness, dissections, serrations, and leaf perimeter.

Conventional geometric morphometric techniques mainly focus on the homologous features that are sensitive to the leaf size rather than leaf shape, which limits their reliable utility in discriminating leaf shapes at taxonomic levels. However, despite slight imperfections, geometric entropy posits a potential method for classifying leaf shapes at a genus level. We hope this could stimulate plant biologists to explore its potential use in taxonomy.

Leaf morphology is an inheritable plant trait and influences light absorption, sap transport, and photosynthesis. Plants optimize leaf patterns to increase energy exchange efficiency and maximize carbon assimilation, reproduction, and resistance. We know the knowledge of complex leaf forms has a vast potential for understanding geometry and its link with energy capture.

Since complex leaves have more adaptive stability in changing environments, we propose our geometric entropy as a derived plant trait to describe leaf complexity and adaptive stability. It will help in artificial leaf design studies to genetically engineer optimal leaf shapes in the future.

This story is part of Science X Dialog, where researchers can report findings from their published research articles. Visit this page for information about ScienceX Dialog and how to participate.

Vishnu Muraleedharan is a Ph.D. student at the C V Raman Laboratory of Ecological Informatics, Indian Institute of Information Technology and Management – Kerala, India. His research focuses on quantitative approaches to explore the morphological diversity of plant leaves as functional traits.

Sajeev C Rajan is a Ph.D. student at the C V Raman Laboratory of Ecological Informatics, Indian Institute of Information Technology and Management – Kerala, India.

Jaishanker R is an Ecological Physicist and Professor working at the School of Ecology and Environment Studies, Nalanda University, Bihar, India. Previously, Jaishanker was working as a Professor at the School of Informatics, Digital University Kerala.