This article has been reviewed according to Science X's editorial process and policies. Editors have highlighted the following attributes while ensuring the content's credibility:
fact-checked
peer-reviewed publication
trusted source
proofread
Understanding complex systems like the brain by analyzing the hidden geometry of their networks
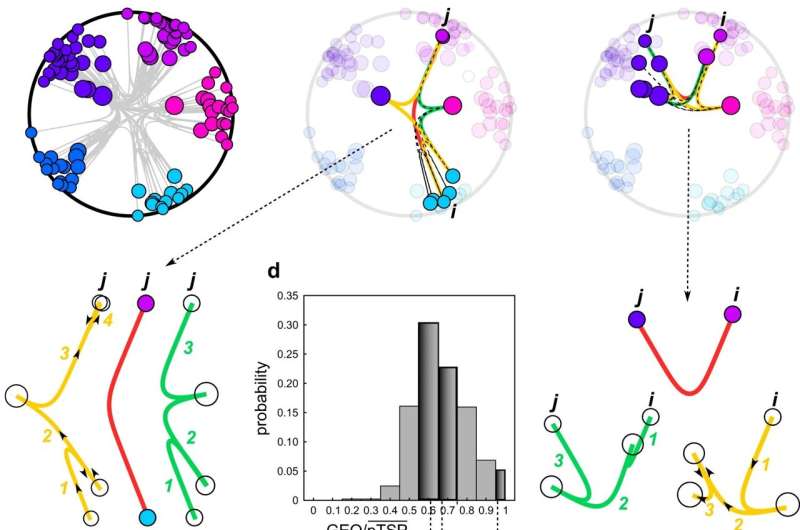
A study published in Nature Communications and directed by Professor Carlo Vittorio Cannistraci, Director of the Center for Complex Network Intelligence (CCNI) at the Tsinghua Laboratory of Brain and Intelligence, proposes a fast algorithm to measure the relation between the variables space of an interconnected complex system, its geometry and its navigability, revealing how this can enhance our understanding of brain differences across age and sex.
Many variables shape the connectivity of networks associated with complex systems such as human society. Some of these variables are known—for instance the higher the popularity of a person, the larger the number of connections they can have in social media networks.
Another example is given by variables such as semantic or spatial proximity. The more people share common interests or live in geographically proximal area, the higher the probability that they link and cluster together forming small and medium communities in a network.
If variables such as popularity and proximity are known, many other variables that shape the connectivity of the network in a complex system are unknown. However the geometrical relation of these variables in a multidimensional space, which we call manifold, remains imprinted as a "trace" in the network structure.
Prof. Carlo Vittorio Cannistraci, the first author of the study, says that "If physics studies the principles and mechanisms of the outside universe, brain science studies the principles and mechanisms of the inside universe. My research is at the interface between these two disciplines. I deal with Physics and Engineering of Complexity and Intelligence: studying principles of natural and artificial intelligence."
In the study that has now been published Nature Communications he envisioned and realized, together with the colleague and co-author Alessandro Muscoloni, how to build an optimized algorithm that reduces 26 years of computation to 1 week, and being able to measure the extent to which a network topology is congruent with an associated manifold geometry.
The manifold represents the rule of geometrical associations between all the variables that contribute to form the network's shape in a complex system, and the network is a sort of discretization of this manifold. The hidden geometry of the manifold behind the structure of brain networks is unknown.
"Although we visualize brain networks in a three-dimensional space, the number of variables that shape their architecture is higher. Some of these variables such as age and sex are known, but many others are unknown, nevertheless we can still find their trace in the shape of the brain network, therefore we can try to measure how congruent is the shape of a network with its hidden geometry. This measure can be used as a marker that can differentiate different states or conditions of brain networks, and therefore can help to envision new theories and measures to design markers for brain diseases," says Cannistraci.
More information: Carlo Vittorio Cannistraci et al, Geometrical congruence, greedy navigability and myopic transfer in complex networks and brain connectomes, Nature Communications (2022). DOI: 10.1038/s41467-022-34634-6
Journal information: Nature Communications
Provided by Tsinghua University