December 10, 2020 feature
Network isotopy: A framework to study the 3-D layouts of physical networks
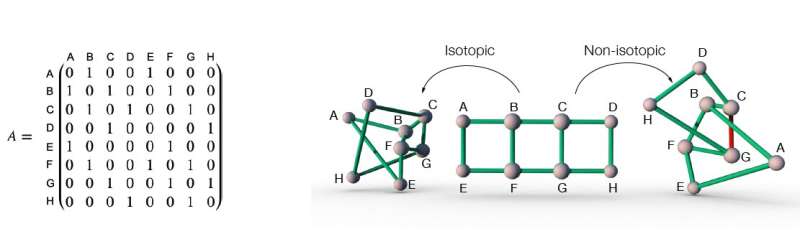
The structure and functions of many physical networks, including the human brain, the vascular system and other biological networks, often depend on their three-dimensional and geometrical layout. Distinguishing between physical networks with identical connections but different geometrical layouts, however, can be very challenging.
Researchers at Northeastern University have recently introduced a theoretical construct called network isotopy that could help scientists to differentiate between physical networks. Network isotopy offers a classification tool that outlines classes of 3-D network layouts that can be transformed into one another without link crossings.
"Our project started out as a curiosity about network layouts," Yanchen Liu, one of the researchers who carried out the study, told Phys.org. "There are many 3-D-printed networks in our office that were studied in various projects in the lab. When looking at these networks, we wondered: If for a given network (fixed wiring of the links) there are infinite ways to place the nodes and links in 3-D space, how can we tell whether two layouts of the same network are the same or different? Moreover, how should we define the similarities between network layouts and if two layouts are different, how should we measure the level of difference between them?"
Shortly after they started conducting their research, Liu and her colleagues realized that there are two main ways in which network geometrical layouts can differ from one another. The first of these depends on the extent to which a network's layout is stretched, while the second results from so-called link-crossing (i.e., links passing through one another).
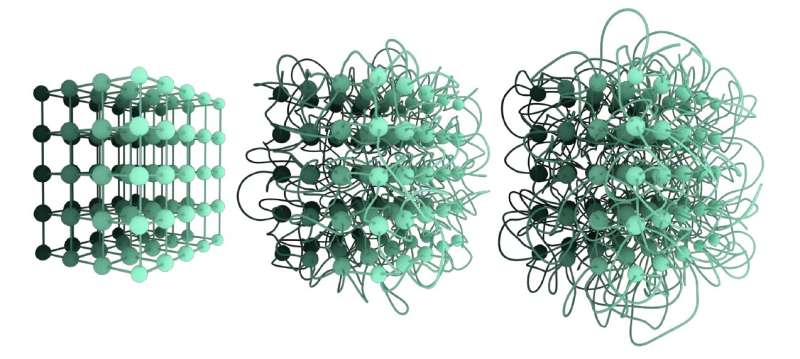
"The first type of difference is trivial, but the second type of difference is intriguing," Liu explained. "Similar questions have been studied in knot theory, which is a field dedicated to knots formed by one or more closed curves."
A physical network's embedding (i.e., layout) is essentially a description of how its nodes and links are put together in space. In their paper, Liu and her colleagues introduced a concept called network-embedding isotopy that can be used to distinguish between different possible embeddings of a given network in 3-D space.
"If two network embeddings are isotopic to each other, it means that they can be stretched into one another without having to cut any link open to let other links pass through," Liu said. "On the other hand, if two network embeddings are non-isotopic to each other, it means that they can never be transformed continuously into one another without cutting links."
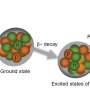
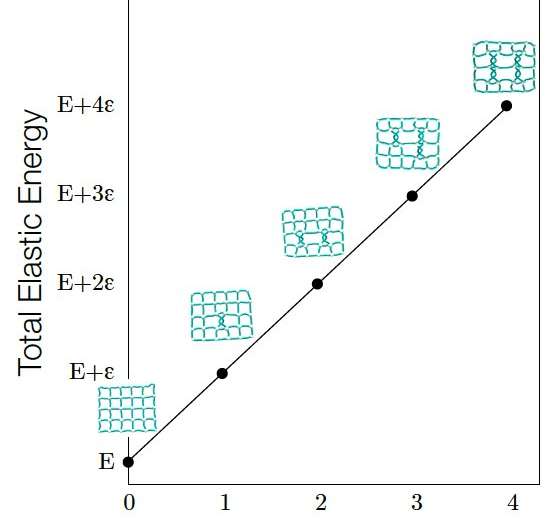
The notion of network isotopy, as it is defined by this team of researchers, can be used to measure the extent to which different network embeddings are tangled, a measure referred to as the graph linking number. Interestingly, Liu and her colleagues found that this measure is also correlated with a layout's elastic energy.
Many physical systems can be described as networks, a significant portion of which are physical networks. The theoretical concepts introduced by the researchers are effective tools to study the properties and geometrical characteristics of these systems.
"There are three important achievements in this paper, in my opinion," Liu said. "The first one is that we defined network embedding isotopy, which is an extension of knot isotopy from knot theory to network embeddings. The second is that we invented the graph linking number, a useful measure of the level of tangledness of network embeddings. Finally, we found that the graph linking number of a network embedding is correlated with the elastic energy of that network embedding."
Liu and her colleagues used their findings to develop a statistical model that describes the formation of tangles in a physical network. In the future, this model could be used to evaluate the extent to which the 3-D layout of a physical system is tangled.
In their recent paper, for instance, the researchers used it to examine the tangledness of many physical systems, including the mouse brain. As all the theoretical constructs introduced in this paper can be applied to a wide variety of physical networks, they could ultimately support physics research focusing on a wide range of topics.
"We are now continuing the study of physical networks," Liu said. "Currently, I am working on one specific physical network: the fruit fly larval brain network, which is a network formed by neurons embedded in 3-D space. We are specifically interested in the connections between the physicality of this network (its embedding) and its structural properties (how the neurons are connected through neuronal wirings)."
More information: Yanchen Liu et al. Isotopy and energy of physical networks, Nature Physics (2020). DOI: 10.1038/s41567-020-1029-z
Journal information: Nature Physics
Provided by Science X Network
© 2020 Science X Network