October 31, 2022 feature
Topological near fields generated by topological structures
Metamaterials and metaoptics offer a broad dimension to explore exotic functionalities in physics and optics. In a new report now published in Science Advances, Jie Peng and a team of scientists in physics and interdisciplinary studies at the City University of Hong Kong, China, discovered how the topology of structures can dictate the properties of optical fields to offer a new dimension of exploration in optic functionalities.
The nontrivial topology of metal structures facilitated the birth of polarization singularities, and the outcomes of the study bridge singular optics, topological photonics, and non-Hermitian physis for applications across chiral sensing, quantum optics and photonics.
A universal connection between topology and optical structures
The concept of topology can provide new perspectives for physicists to explore unconventional properties of one-way edge states in topological insulators and their counterparts. The distribution of polarization ellipses can form topological defects known as polarization singularities, which emerge during applications such as light focusing, scattering and interference in nanostructures including meta-surfaces and photonic crystals. The geometry of optical structures can still decide the local resonance of optical modes to give rise to new optical devices including nano-antennas, metamaterials and metasurfaces.
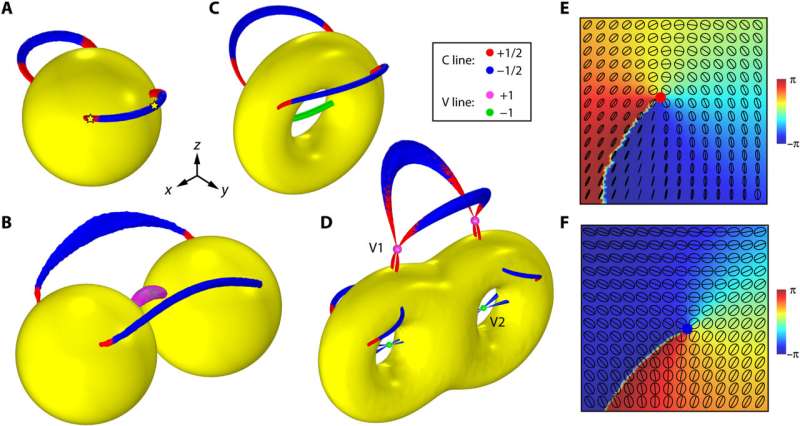
In this work, Peng et al. established a universal and exact connection between topology and optical structures to reveal how the origin and topological evolution of magnetic polarization in the near fields were bound by the topology and symmetry of the structures.
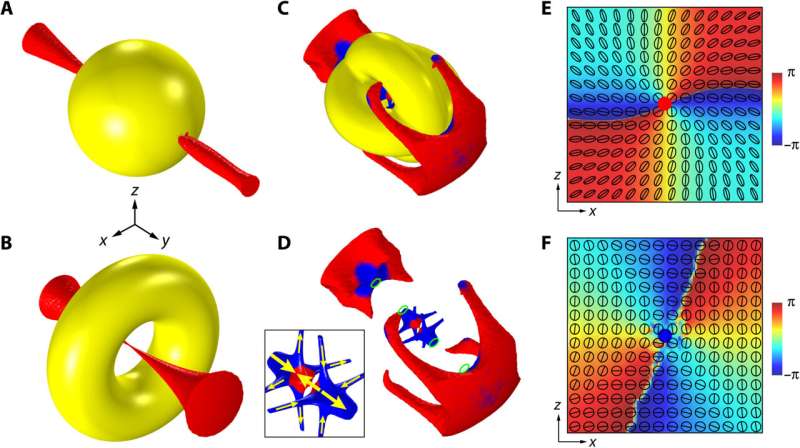
Polarization singularities protected by surface topology of structures
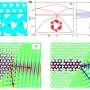
The team conducted full-wave numerical simulations of the system by using a finite-element package via COMSOL Multiphysics. During the experiments, they considered a metal sphere under the incidence of a plane propagating in the z direction with a magnetic field linearly polarized in the y direction. They then determined polarization singularities emerging in the total magnetic field.
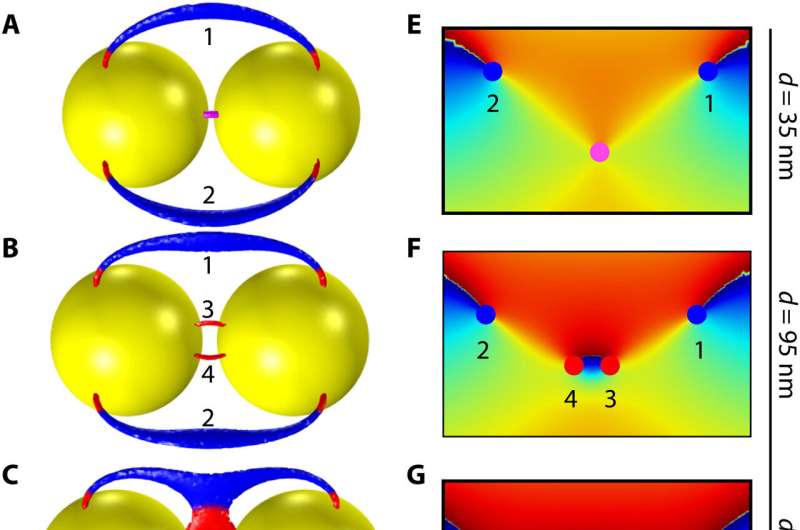
Peng and the team further sought to understand the underlying basis of the morphologies of PSLs, which they found in topological properties associated with the geometry of metal spheres. For example, the excitation of the incident electromagnetic field induced currents in metal structures, mainly localized in a thin surface layer of the structures. The study outcomes established a direct link between the topology of optical structures and topological properties of optical near-fields, applicable for arbitrary metal structures with smooth geometric surfaces and small skin depth. The emergence of polarization singularities was further protected by the topology of the structures; therefore, their properties were robust against continued variations of the geometric structures.
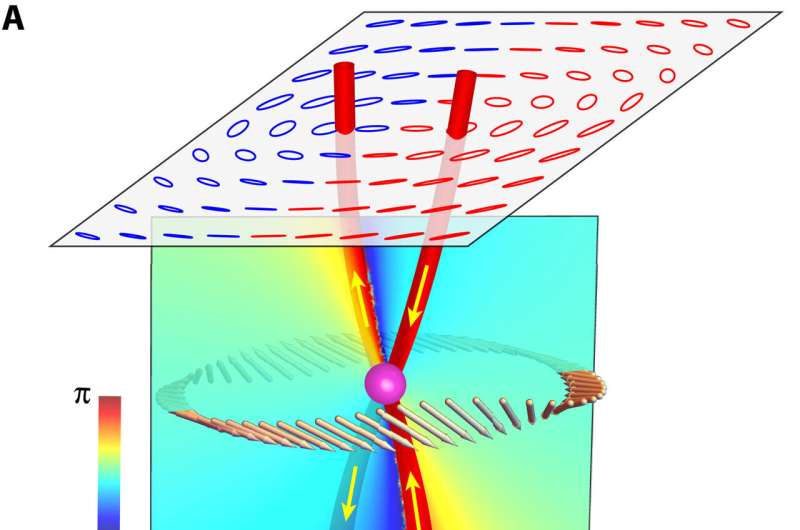
Topology and mirror symmetry vs. topology and generalized rotational symmetry
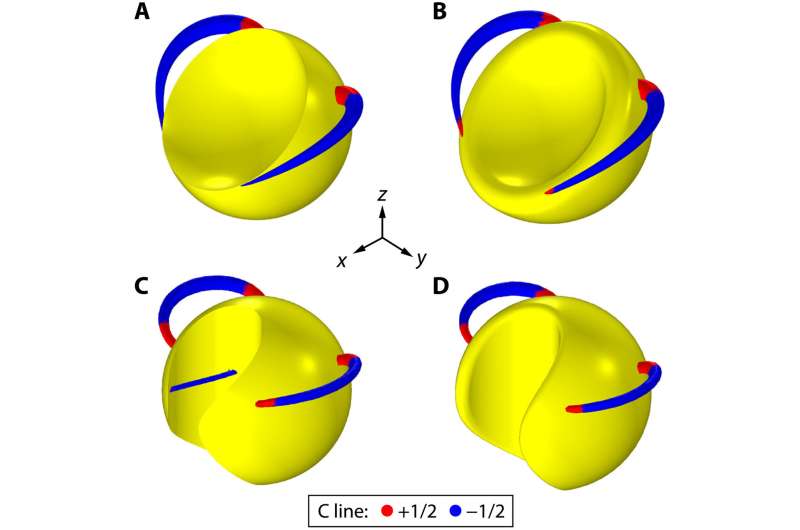
The scientists noted how the polarization singularities further evolved as they extended away from the surface of the structures to merge, bifurcate and transition in the three-dimensional space. The team examined topological transitions of polarization singularities and further examined the properties of polarization singularities by discussing the combined effects of mirror symmetry and topology.
The study outcomes emphasized the significance of spatial symmetry to engender the topologically complex polarization configurations that could not stably exist in non-symmetry. The researchers noted how the higher order polarization singularities and polarization singularity lines were typically unstable without symmetry protection to transform into the lowest order under perturbations.
Outlook
In this way, Jie Peng and colleagues showed a direct relationship between the topology of metal structures and magnetic polarization singularity lines in the near-field. The study highlighted exotic topological properties of optical polarization fields that are irrelevant to the specific material or geometry of optical structures. The outcomes are connected to polarization singularities as well as topological symmetry of structures and non-Hermitian physics.
The study opens new opportunities for fundamental explorations in discerning chiral counterparts for sensing applications in chiral quantum optics and topological photonics. The team envision extending these outcomes to classical wave systems, including sound waves and water surface waves.
More information: Jie Peng et al, Topological near fields generated by topological structures, Science Advances (2022). DOI: 10.1126/sciadv.abq0910
Danica Sugic et al, Particle-like topologies in light, Nature Communications (2021). DOI: 10.1038/s41467-021-26171-5
Journal information: Nature Communications , Science Advances
© 2022 Science X Network