Complex patterns: Building a bridge from the large to the small

For many processes important for life such as cell division, cell migration, and the development of organs, the spatially and temporally correct formation of biological patterns is essential. To understand these processes, the principal task consists not in explaining how patterns form out of a homogeneous initial condition, but in explaining how simple patterns change into increasingly complex ones. Illuminating the mechanisms of this complex self-organization on various spatial and temporal scales is a key challenge for science.

So-called "coarse-graining" techniques allow such multiscale systems to be simplified, such that they can be described with a reduced model at large length and time scales. "The price you pay for coarse-graining, however, is that important information about the patterns on small scales—like the pattern type—is lost. But the thing is that these patterns play a decisive role in biological systems. To give one example, they control important cellular processes," explains Laeschkir Würthner, member of the team led by LMU physicist Prof. Erwin Frey and lead author of a new study published in the Proceedings of the National Academy of Sciences that overcomes this issue.

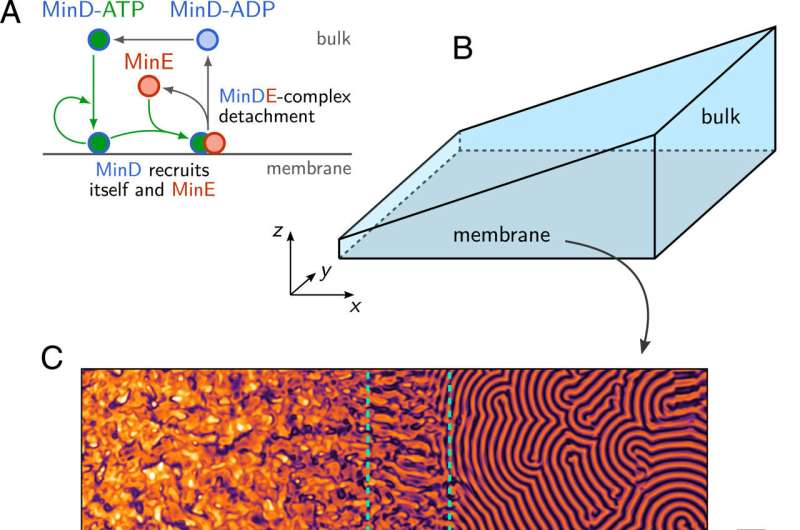
In collaboration with the research group of Prof. Cees Dekker (TU Delft), Frey's team has developed a new coarse-graining approach for so-called mass-conserving reaction-diffusion systems, in which the large-scale analysis of the total densities of the particles involved enables the prediction of patterns on small scales.

The scientists illustrated the potential of their approach with the Min protein system, a paradigmatic model for biological pattern formation. The bacterium E. coli uses various Min proteins circulating in a cell to determine at which location cell division takes place. A decisive factor here is that the proteins involved occur at different frequencies depending on their location in the cell and chemical state—which is to say, they have a variety of different densities.

"We've now managed to reduce the complexity of this system by developing a theory that is based solely on the total densities of the proteins, such that we can completely mirror the dynamics of pattern formation," says Frey. "This is a huge reduction. The numerical computations are now accomplished in a matter of minutes instead of months."

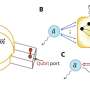
The researchers were able to experimentally confirm theoretical predictions of the model, according to which distribution of the proteins depends on the geometry of the environment. They did this by reconstructing the Min protein system in an in-vitro flow cell, with the results showing the same protein patterns as were revealed in the simulation.

"Such reconstruction of information at a small length scale from reduced dynamics at the macroscopic level opens up new pathways for a better understanding of complex multiscale systems, which occur in a broad range of physical systems," says Frey.