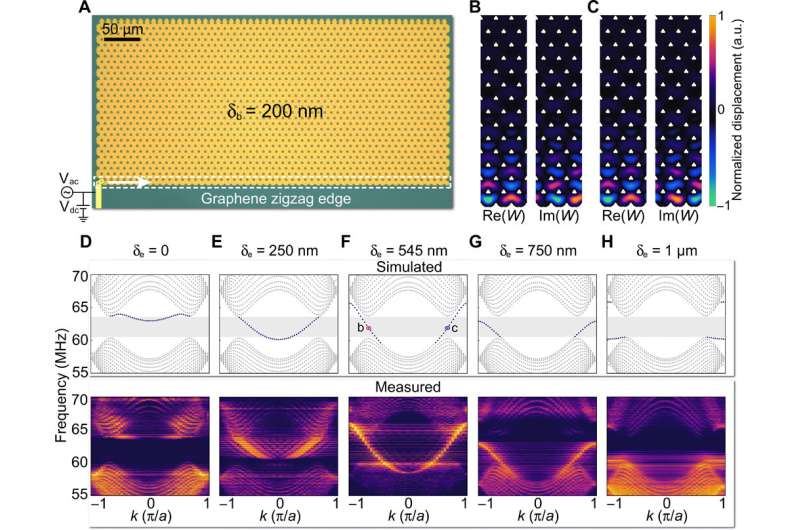
January 22, 2021 feature
Observing chiral edge states in gapped nanomechanical graphene
Edge states are an emerging concept in physics and have been explored as an efficient strategy to manipulate electrons, photons and phonons for next-generation hybrid electro-optomechanical circuits. Scientists have used gapless chiral edge states in graphene or graphene-like materials to understand exotic quantum phenomena such as quantum spin or valley Hall effects. In a new report now published on Science Advances, Xiang Xi and colleagues reported on experimental chiral edge states in gapped nanomechanical graphene; a honeycomb lattice of free-standing silicon nitride nanomechanical membranes with broken spatial inversion symmetry (presence of a dipole). The constructs were immune against backscattering in sharp bends and exhibited the valley-momentum locking effect. The team realized a smooth transition between the chiral edge states and the well-known valley kink states to open the door for experimental investigations of soft graphene-related physics in very-high-frequency, integrated nanomechanical systems.
Developing nanomechanical graphene
The presence of chiral edge states at the boundary of two-dimensional (2-D) materials is an intriguing phenomenon in condensed matter physics. Well-known examples include quantum Hall (QH) or quantum spin Hall effects (QSH), where the chiral edge states act as gapless backscattering immune-conducting channels even with insulating interiors. Graphene is an ideal 2-D material that has attracted extensive interests since its first experimental realization. Zigzag-terminated graphene can support a flat-band edge state at its boundary leading to a variety of phenomena including magnetism and superconductivity. The chiral edge states in graphene can be observed experimentally due to the quantum Hall effect with an external magnetic field, although it is also possible to harness the quantum spin Hall effect without an external magnetic field. However, the weak spin-orbit interaction had made the experimental realization of in graphene chiral edge states an outstanding challenge. Researchers had previously proposed the quantum valley Hall effect (QVH) as an alternative strategy to realize chiral edge states in graphene. In this work, Xi et al. experimentally realized the quantum valley chiral edge states by constructing a gapped nanomechanical graphene 2-D honeycomb lattice of free-standing silicon nitride nanomechanical membranes functioning at a very high band frequency regime. The team tuned the conventional gapped flat-band graphene edge states to gapless chiral states to develop a nanomechanical system that can generate graphene-related physics with electrical tunability and strong nonlinearity.
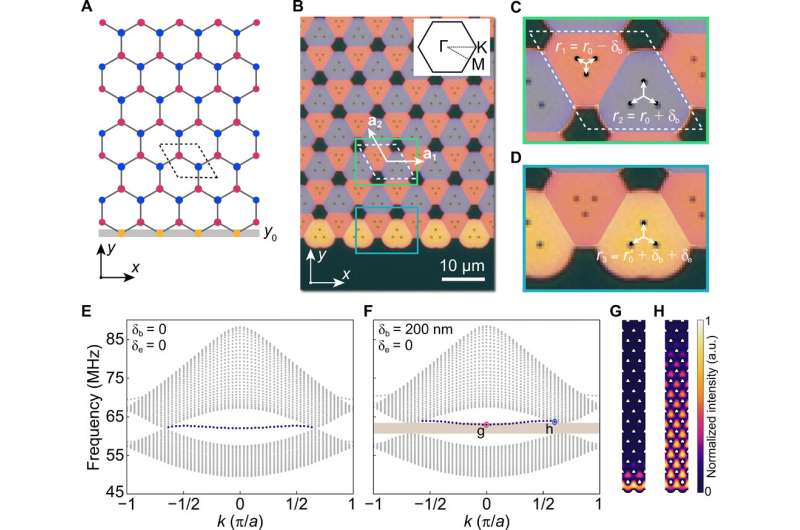
Controlling the nanomechanical graphene edge states by the boundary potential
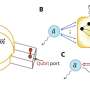
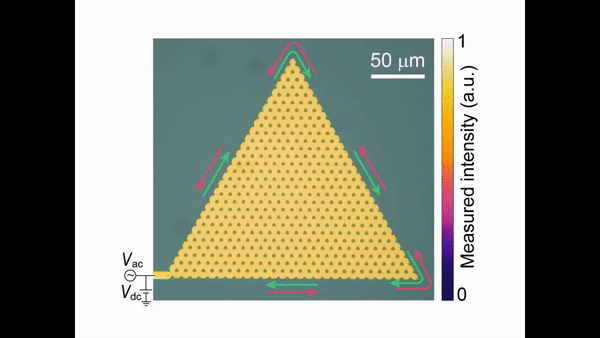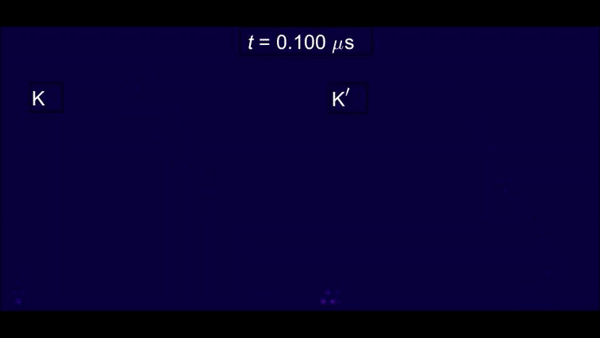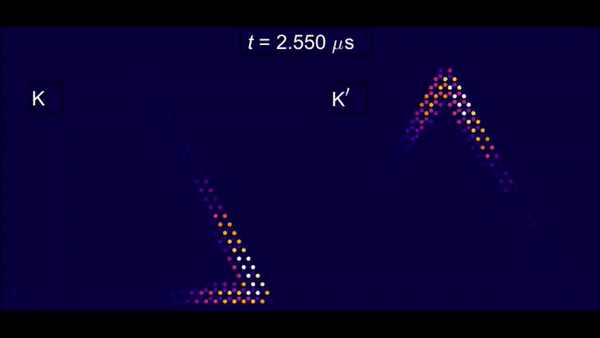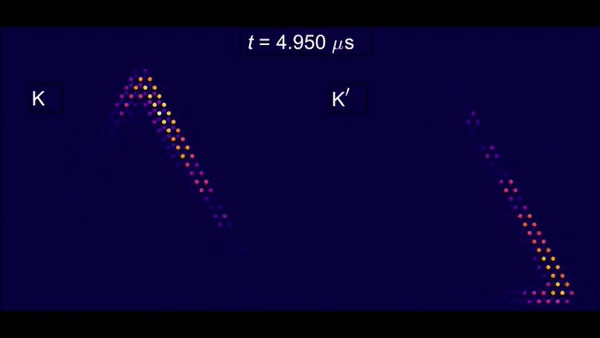
The generic graphene lattice used in this work contained a zigzag edge and a nanomechanical honeycomb lattice architecture. The team experimentally realized the gapped nanomechanical graphene to observe chiral edge states with quantum valley Hall effects (QVH). For this, they constructed a 2-D array of silicon nitride membranes in a honeycomb lattice. They first fabricated materials on a silicon-nitride-on-insulator wafer by etching small holes in the silicon nitride layer and ultimately found the bulk region of the nanomechanical graphene to exhibit the expected QVH effects with nontrivial valley Chern numbers (Chern numbers can provide information about the wavefunction). Ge et al. then developed extensive theoretical analyses to form the basis to experimentally realize chiral edge states in nanomechanical graphene. The energy response of the edge states differed with the boundary potential to provide an intuitive explanation to control the dispersion of the energy states within the architecture.
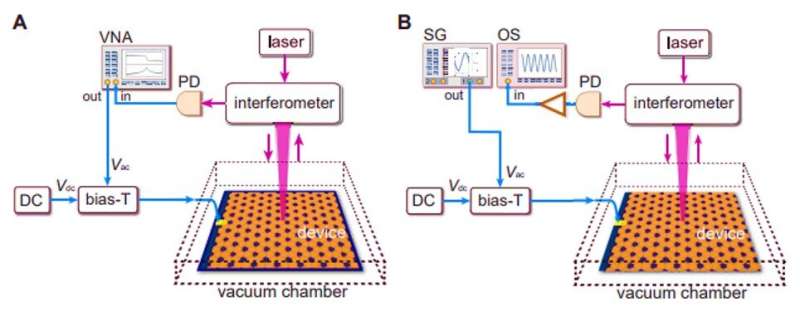
The team showed the experimental controllability by tuning the on-site potential at the zig-zag edges of the gapped nanomechanical graphene. During the process, they triggered the flexural motions of the membranes electrocapacitively by using a combination of constant voltage Vdc and alternating voltage Vac, applied to the excitation electrode and measured optically with a homebuilt Michelson interferometer functioning at an optical wavelength of 1570 nm. They phase-locked the detecting beam and the reference beam in the interferometer by using a kilohertz proportional-integral-derivative controller. They then used a vector network analyser to detect the frequency response of the devices and measured the signals from the photodetector using an oscilloscope synchronized with the signal detector. During the experiments, they focused on the graphene edge states and their transition to chiral edge states and characterized the chiral edge states along a closed-loop, triangle-shaped boundary.
Gapless edge states and valley kink states
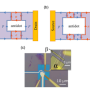
Xi et al. next experimentally imaged the spatiotemporal profiles of the elastic waves driven by a pulse-modulated Vac signal in the setup with a carrier frequency of 64.65 MHz, a pulse width of 1 µs and a pulse repetition rate of 1 KHz and found the gapless edge states to exhibit chiral propagation. Most importantly, the gapless edge states propagated smoothly through sharp bends without backscatter. Similar gapless valley-dependent chiral modes could also exist at the topological domain walls of the device between two graphene regions with opposite valley Chern numbers, referred to as valley kink states. Such states were previously demonstrated in bulk acoustic and mechanical systems alone, and not in nanomechanics. Xi et al. then experimentally showed the nanomechanical valley kink states and smooth transitions between the chiral edge states and valley kink states.
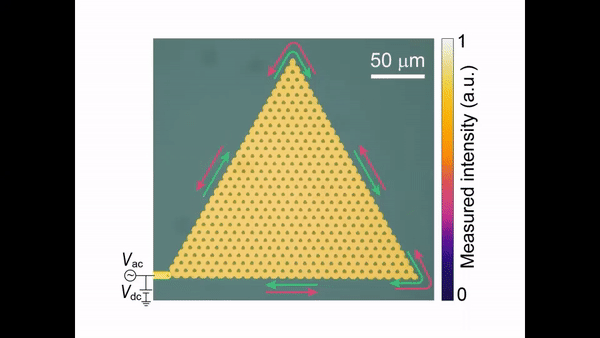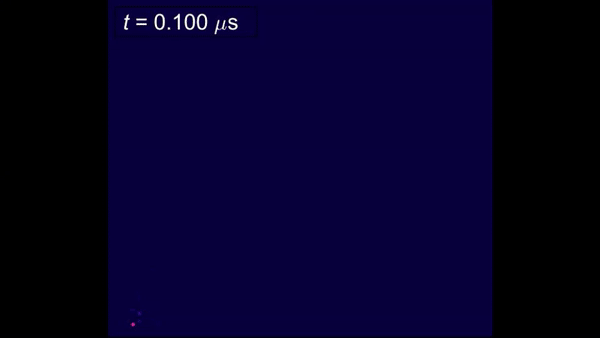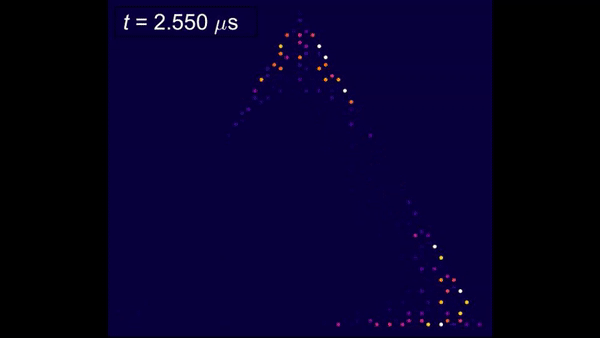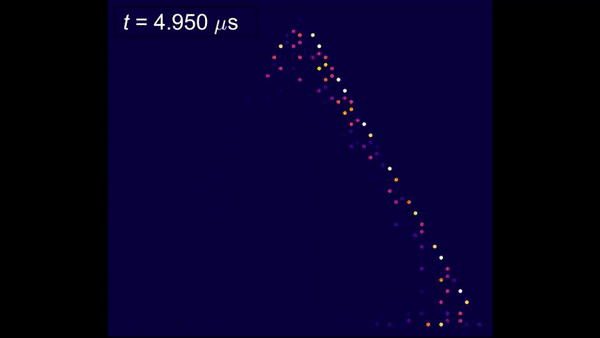
They explored the valley kink states and their similarity to chiral edge states by designing and fabricating another device with gapped nanomechanical graphene and experimentally imaged the space-time profiles of the elastic waves in the setup. The setup contained a pulse-modulated Vac signal with a carrier frequency of 60.53 MHz, a pulse width of 1.5 µs and a pulse repetition rate of 1 KHz. The elastic waves in the chiral edge states then smoothly transformed into the valley kink states and propagated along the domain walls of the device and transformed back into the chiral edge states without undergoing undesired backscattering.
Outlook for nanomechanics
In this way, Xiang Xi and colleagues introduced the concept of graphene and the quantum valley Hall (QVH) chiral-edge states by accurately controlling the boundary potentials of the graphene lattice. The researchers confirmed the states to be topologically immune against sharp bends while exhibiting valley-momentum locking, much like quantum spin Hall (QSH) systems. Xi et al. realized smooth transition between chiral edges states and well-known valley kink states. The chiral edge states also demonstrated a smaller footprint, demonstrating the capacity to enable more compact topological circuits in practice. The results provide a new strategy to construct a variety of integrated nanomechanical circuits functioning at very-high-frequency regimes including unidirectional waveguides and topologically protected high-quality cavities. The work will open new doors to explore nonlinear phononics in graphene-like systems including graphene-edge solitons , amplifiers and lasers.
More information: Xi X. et al. Observation of chiral edge states in gapped nanomechanical graphene, Science Advances, DOI: 10.1126/sciadv.abe1398
Hatsugai Y. Chern number and edge states in the integer quantum Hall effect. Physical Review Letters, doi.org/10.1103/PhysRevLett.71.3697
Geim A. K. et al. The rise of graphene. Nature Materials, doi.org/10.1038/nmat1849
Journal information: Nature Materials , Physical Review Letters , Science Advances
© 2021 Science X Network