February 28, 2020 feature
Helical quantum Hall phase in graphene on strontium titanate
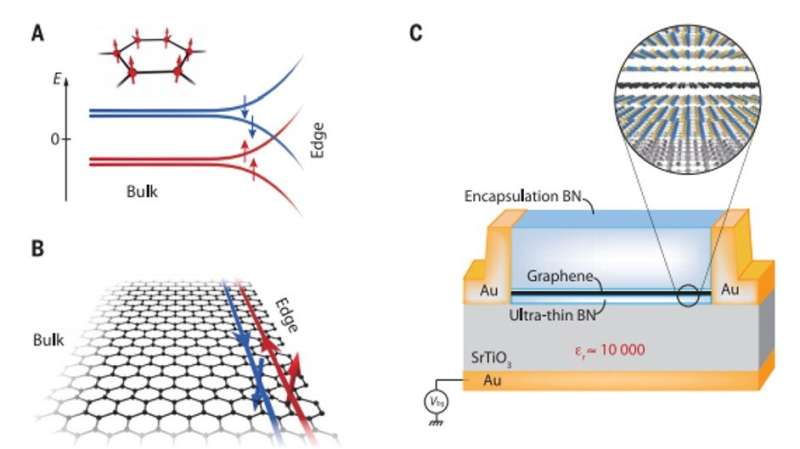
Materials that exhibit topological phases can be classified by their dimensionality, symmetries and topological invariants to form conductive-edge states with peculiar transport and spin properties. For example, the quantum Hall effect can arise in two-dimensional (2-D) electron systems subjected to a perpendicular magnetic field. When distinct characteristics of quantum Hall systems are compared with time-reversal symmetric (entropy conserved) topological insulators (TIs), they appear to rely on Coulomb interactions between electrons to induce a wealth of strongly correlated, topologically or symmetry-projected phases in a variety of experimental systems.
In a new report now on Science, Louis Veyrat and a research team in materials science, quantum optics and optoelectronics in France, China and Japan tuned the ground state of the graphene zeroth Landau level i.e. orbitals occupied by charged particles with discrete energy values. Using suitable screening of the Coulomb interaction with the high dielectric constant of a strontium titanate (SrTiO3) substrate, they observed robust helical edge transport at magnetic fields as low as 1 Tesla, withstanding temperatures of up to 110 kelvin across micron-long distances. These versatile graphene platforms will have applications in spintronics and topological quantum computation.
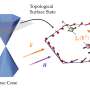
Topological insulators (TIs), i.e., a material that behaves as an insulator in its interior but retains a conducting surface state, with zero Chern number have emerged as quantum Hall topological insulators (QHTIs) arising from many-body interacting Landau levels. They can be pictured as two independent copies of quantum Hall systems with opposite chirality, but the experimental system is at odds with the described scenario, where a strong insulating state is observed on increasing the perpendicular magnetic field in charge-neutral, high-mobility graphene devices.
The experimental formation of the ferromagnetic (F) phase (F-phase) in graphene is therefore potentially hindered by such lattice-scale electron-electron and electron-phonon interactions. To overcome this, scientists had previously applied a very strong in-plane magnetic field component higher than 30 Tesla to surpass anisotropic interactions, allowing the F-phase to experimentally emerge in graphene. In another strategy they used graphene bilayers hosting two different quantum Hall states of opposite charge-carrier types, but they suffered from an impractically strong and tilted magnetic field or complexity of materials assembly. As a result, in this work Veyrat et al. used a different approach to induce the F-phase in monolayer graphene. Instead of boosting the Zeeman energy or Zeeman effect i.e. splitting a spectral line using a magnetic field to overcome anisotropic interactions, they modified the lattice-scale interactions relative to Coulomb interactions to restore the dominant role of the spin-polarizing terms and induce the F-phase.
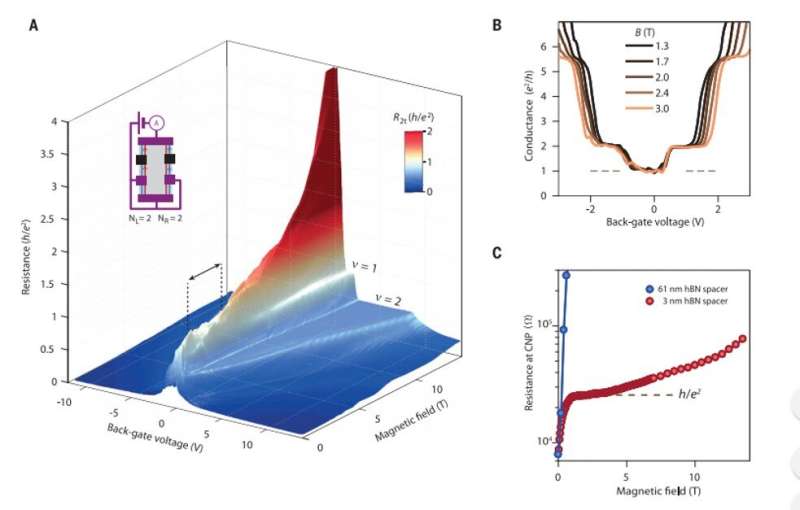
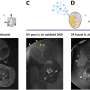
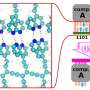
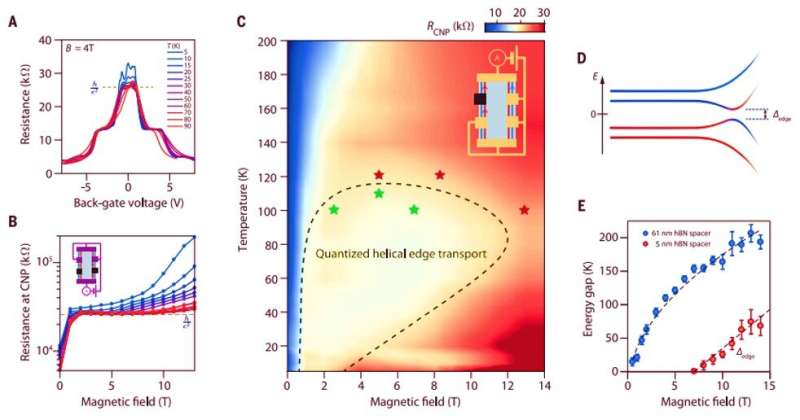
For this, they used quantum paraelectric strontium titanate (SrTiO3), known to exhibit a large static dielectric constant (D≈104) at low temperatures. The setup eventually modified the ground state of graphene at charge neutrality. Veyrat et al. accomplished this by engineering high-mobility graphene heterostructures based on hexagonal boron nitride (hBN) encapsulation and readily observed the emergence of the F-phase in a screened configuration. By changing the source of electrons and drain (flow of electrons) contacts in the setup, and the number of helical edge sections, they observed helical edge transport. Veyrat et al. also observed simultaneous measurements of two-terminal resistances and non-local resistance while keeping the same source and drain current-injection contacts to demonstrate current flow on the edges of the sample.
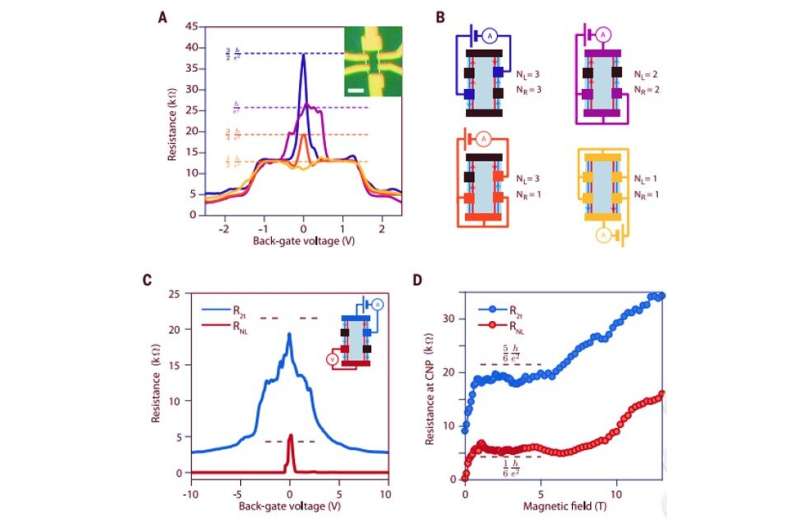
To investigate robustness of helical edge transport, the team conducted systematic studies of its temperature and magnetic field dependence. The SrTiO3 dielectric constant remained high enough up to 200 K, and the dielectric screening remained virtually unaffected. To understand the limit of quantized helical edge transport, the team measured different contact configurations at several magnetic field and temperature values to show that quantized helical edge transport could withstand very high temperatures of up to 110 K.
The team then demonstrated the key role of the SrTiO3 dielectric substrate during F-phase establishment. Due to substantially reduced electron-electron interactions in a high-dielectric constant measurement, the F-phase emerged as a ground state in the control experiments. Veyrat et al. further investigated the screening effects and short-range lattice-scale contributions of the Coulomb and electron-phonon interactions to determine the energetically favorable ground state. The observed mechanisms will open exciting new perspectives. For instance, the Coulomb energy scale could be enhanced by increasing the magnetic field to induce a topological quantum phase transition from the QHTI (quantum Hall topological insulators) ferromagnetic phase to an insulating, trivial quantum Hall ground state—a type of transition hitherto little addressed.
In this way, Louis Veyrat and colleagues demonstrated the ferromagnetic (F) phase in screened graphene. The setup emerged at low magnetic fields as a prototypical interaction-induced topological phase with robust helical edge transport. The edge excitations were tunable with magnetic fields to study zero-energy modes in superconductivity-proximitized architectures. The method of substrate-screening engineering was tunable due to the thickness of the hBN spacer used in the study, the team therefore expect the ground states and optoelectronic properties of other correlated 2-D systems to be as strongly influenced by their dielectric environment.
More information: Louis Veyrat et al. Helical quantum Hall phase in graphene on SrTiO3, Science (2020). DOI: 10.1126/science.aax8201
Javier D. Sanchez-Yamagishi et al. Helical edge states and fractional quantum Hall effect in a graphene electron–hole bilayer, Nature Nanotechnology (2016). DOI: 10.1038/nnano.2016.214
A. F. Young et al. Tunable symmetry breaking and helical edge transport in a graphene quantum spin Hall state, Nature (2013). DOI: 10.1038/nature12800
Journal information: Science , Nature Nanotechnology , Nature
© 2020 Science X Network