New class of spongy materials can self-assemble into precisely controllable structures

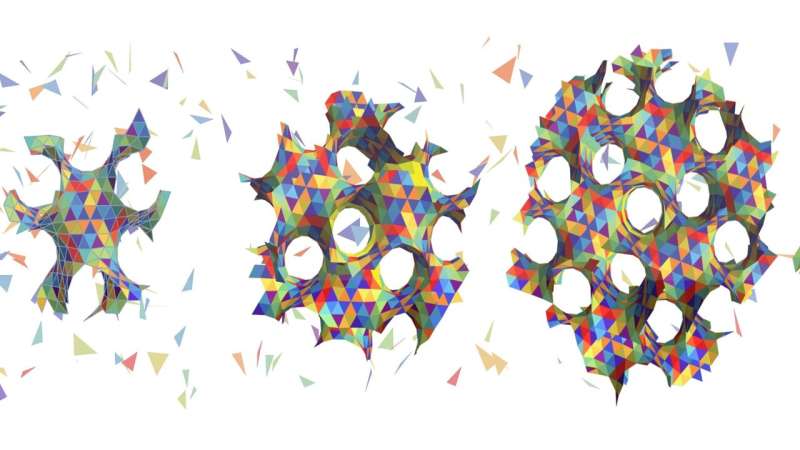
A team of researchers led by the University of Massachusetts Amherst has drawn inspiration from a wide variety of natural geometric motifs—including those of 12-sided dice and potato chips—in order to extend a set of well-known design principles to an entirely new class of spongy materials that can self-assemble into precisely controllable structures.

Their theory and computational model, published in the Proceedings of the National Academy of Sciences, allows for maximum design economy, or the largest possible structure using the fewest number of programmable, self-assembling pieces.

One of the holy grails of materials science is to emulate nature's ability to form robust, complex self-assembling materials that can then create structures capable of a wide range of functions. Think of the crystalline nanostructures that form on a butterfly's wings and whose precise form and size determine exactly which wavelengths of light to reflect, giving different species their distinctive markings.

"We were inspired by virus self-assembly," says Greg Grason, professor of polymer science at UMass Amherst and the paper's senior author.

"Though some viruses can pose risks from a health perspective, they have an incredible 'self-closing' design. Many have a rigid, highly symmetric spherical shell, and this shell is built of the fewest number of protein arrangements possible. The shell is also just the right size—any bigger, and it wouldn't be able to infect its host; any smaller, and the virus wouldn't be powerful enough. We want to be able to create materials that can economically self-assemble into the perfect shape, just like viruses—except we want to engineer entirely different types of geometries."

Grason and his team, including colleagues at Brandeis and Syracuse universities, as well as co-lead authors Carlos M. Duque and Douglas M. Hall, both of whom completed this research as part of their graduate studies at UMass Amherst, are hardly the first to be inspired by viruses.

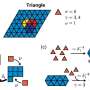
Back in the 1960s, a pair of structural biologists named Donald Caspar and Nobel Prize winner Aaron Klug, inspired by Buckminster Fuller's famous geodesic domes, realized that the structure of his domes also described virus shells. They went on to derive a set of design principles, called the Caspar-Klug symmetry principles, that describe how to build a structure enclosing the largest possible volume with the fewest number of building blocks.

"Inspired by the beauty and elegance of the Caspar-Klug construction for icosahedral viral shells, we developed a roadmap to find economical design rules that can help us engineer a wide range of very useful nanostructures," says Duque.

However, the Caspar-Klug symmetry principle only describes structures with positive curvatures, or shapes, like a dome, that curve inward in every direction.

"We wondered what would happen if you invert the curvature so that the curves run in opposite directions from each other, like a Pringles potato chip," says Grason.

"What types of self-closing geometries could form with negative curvature, and could they preserve the economy of the Caspar-Klug assembly?"

Structures with this kind of negative curvature have a spongy structure built of interconnected holes and tubes, and are in fact, closely related to the photonic nanostructures formed in butterfly wing scales.

To answer their questions, Grason and his co-authors designed a computational model, which showed that structures with a triply periodic negative curvature could indeed preserve the economy of assembly that Caspar and Klug observed in spherical viruses.

"We're able to extend the economics of shapes with a positive curvature to a much more complex set of structures that can be realized by assembling 'programmable' building blocks that can be made using the approaches of DNA nanotechnology, or de novo protein design," says Grason.

"Our work models the process of assembly," says Hall.

"First, a few building blocks come together to make a negatively curved patch, like a potato chip with rough edges. As the patch grows, the surface closes in on itself and forms channels that extend in all three dimensions. The highly regular array of channels is what allows for new potential materials with brilliant color or the ability to attenuate sounds."