Team solves old mystery, paving way toward advances in medicine, industry, environmental science

An Oregon State University environmental engineering professor has solved a decades-old mystery regarding the behavior of fluids, a field of study with widespread medical, industrial and environmental applications.
The research by Brian D. Wood, published in the Journal of Fluid Mechanics, clears a roadblock that has been puzzling scientific minds for nearly 70 years and paves the way to a clearer picture of how chemicals mix in fluids.
A more complete grasp of that basic principle provides a foundation for advances in a range of areas—from how pollutants spread in the atmosphere to how drugs perfuse tissues within the human body.
Funded by the National Science Foundation, Wood's work with dispersion theory builds on research by one of the most accomplished scientists in Oregon State history, Octave Levenspiel. A 1952 chemical engineering Ph.D. graduate and later a longtime faculty member, Levenspiel in 1957 published an important paper on dispersion in chemical reactors on his way to becoming the college's first inductee to the National Academy of Engineering.
Even more importantly, the research by Wood bridges a longstanding gap in one of the fundamental tenets of fluid mechanics: Taylor dispersion theory. Named for British physicist and mathematician G.I. Taylor, author of a seminal 1953 paper, the theory concerns phenomena in which fluctuations in a fluid's velocity fields cause chemicals to spread within it.
"The process of dispersive spreading tends to increase over time until it reaches a steady level," Wood said. "You can think of it as analogous to investment in a startup, in which the rates of return can initially be very large before settling in to a more sustainable level that is close to constant."
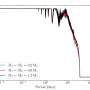
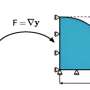
Taylor's theory was the first to allow researchers to predict that steady level of dispersion using what's known as the macroscopic dispersion equation. The equation can describe the net movement of a chemical species in a fluid—provided enough time has elapsed from when the chemical entered the fluid.
"That was a significant revelation at the time," Wood said. "It was on par with what researchers were doing theoretically in other disciplines, like quantum mechanics."
While Taylor's theory was successful and revolutionary, researchers still struggled with the problem of how dispersive spreading evolves from its dynamic, early behavior—what's termed as its initial condition—to when it attains the more constant value predicted by Taylor.
Scientists found some success by adding to the equation a time-dependent dispersion coefficient, but the coefficient created problems of its own, the primary one being paradoxes.
"For example, if chemical solutes injected into a fluid at two different times overlap, which time do you assign to the dispersion coefficient?" Wood said. "Taylor himself understood that, where a time-dependent dispersion coefficient was adopted, contemporary theories violated basic notions of causality in physics."
Wood and collaborators used another canon, the theory of partial differential equations, to show that problems with the time-dependent dispersion coefficient arose from neglecting the relaxation of the solute—the chemical injected into the fluid, or solution—from its initial condition.
"When chemical species are first injected, their behavior is not necessarily consistent with a dispersion-type equation," Wood explained. "Rather, the initial condition first has to 'relax.' During this time, there is an additional term to account for that was missing in Taylor's macroscale dispersion equation."
In an equation, a term refers to a single number or a variable, or numbers and variables multiplied together.
The term Wood added corrects the dispersion equation to account for the initial configuration of the chemical species moving around in the fluid. Somewhat surprisingly, Wood said, the theory also resolves paradoxes in other theories with time-dependent dispersion coefficients.
"In the new theory, there is never a question about what dispersion coefficient should be used when chemical solutes overlap," he said. "The adjustment to the spreading process is accounted for automatically by the presence of the additional term."
More information: E. Taghizadeh et al, Preasymptotic Taylor dispersion: evolution from the initial condition, Journal of Fluid Mechanics (2020). DOI: 10.1017/jfm.2020.56
Journal information: Journal of Fluid Mechanics
Provided by Oregon State University