Mathematician develops method to explore the structure of molecules

A scientist from the Mathematical Laboratory of RUDN University has obtained new results in a study of the inverse problem for coupled Schrödinger equations. This result will be useful for describing the interaction of laser beams and particles with molecules and the analysis of molecular structures. The article is published in Inverse Problems.

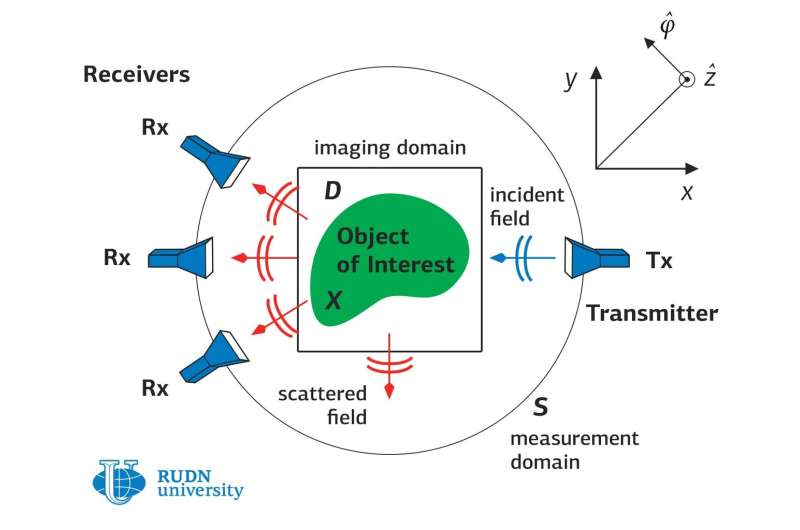
Usually, a mathematical problem comprises an equation that needs to be solved. But in physics, the opposite often happens: Scientists know the results of measurements, but equations describing the properties of the physical system are unknown. This is called an inverse problem—the problem of finding an equation using its solution.

In quantum physics, it is often necessary to solve variants of the inverse scattering problem, for example, to reconstruct the structure of a molecule using the scattering pattern of the particles with which it is fired. In this case, it is necessary to solve the Schrödinger equation for several particles, but this problem is not solved in general.

Therefore, it is necessary to find the measurements to reconstruct the potential uniquely, and create an algorithm by which the potential can be reconstructed numerically. Moreover, even if the numerical method has already been invented, you need to understand whether it is correct and whether it works as it should. Theorems evaluating the potential by measurements are needed to solve these problems.

Masahiro Yamamoto from RUDN University, together with Fangfang Dou from China, obtained such theorems. They investigated coupled Schrödinger equations, previously unstudied, in their research. In previous papers, inverse problems for ordinary and nonlinear Schrödinger equations have been studied. However, coupled Schrödinger equations are a relatively young class of problems. Therefore, their direct problem is investigated, while the reverse is not.

Coupled Schrödinger equations are a system of two Schrödinger equations in which there are additional components responsible for the interaction of radiation and molecules. They are needed to describe recent experiments with the effect of laser radiation on intermolecular bonds in deuterium and hydrogen ions. Masahiro Yamamoto and Fangfang Dou obtained new theorems that allow estimating undisturbed radiation potentials using the results of measurements.

Their new study will allow mathematicians to apply numerical methods to models of multiphoton transitions, which will help us to simulate the change in the properties of chemical bonds under the influence of intense laser fields. Applications of these results for various studies in nanophotonics and mesoscopic physics are likely to arise in the future, because the question of controlling and suppressing the dissociation of molecules with laser radiation has been worrying physicists for a long time.