Mathematician proposes method to simplify the mathematical model of substance transfer through a cell wall
A mathematician from RUDN University has proposed a new scheme for numerically solving equations with fractional powers of elliptic operators. The new scheme works faster than the existing ones, because it takes into account the properties of the solutions to such equations at singular points. The results could be useful for calculating diffusion processes—for example, fluid leakage in a porous medium, transfer of nutrients through a cell wall, and breaks in elastic materials. The study was published in Computers & Mathematics with Applications.
The classical diffusion equation is a partial differential equation. It describes the process of distribution of a substance in a certain environment. The solution to the equation is a function of time t and point x, which shows the concentration u (t, x) of the substance at point x at time t. If the medium is homogeneous, then the diffusion equation contains the first derivative with respect to t of u and the sum of the second derivatives of u with respect to coordinates. The sum is called the Laplace operator, and is used in various fields of mathematics and physics, including the theory of complex functions and the Schrödinger equation.
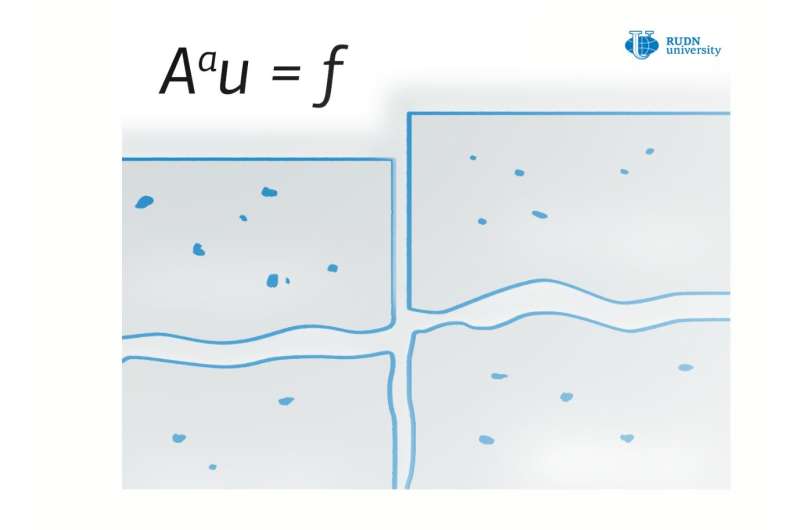
Mathematician Petr Vabishchevich, an employee of the Scientific Center for Computational Methods in Applied Mathematics at RUDN University, and his colleague Raimondas Ciegis, Prof. of Mathematics in Vilnius Gediminas Technical University, Vilnius, Lithuania, considered a variant of the fractional diffusion equation in which the Laplace operator is taken to a fractional degree. The degree is determined by the formula, which is convenient from a theoretical point of view, but completely unsuitable for calculations. In the meantime, practical calculations related to solutions are an important task for applications.
If solving an equation in general form is difficult, mathematicians use numerical methods. There are several of them that are traditionally used for the fractional diffusion equation. For example, one of them assumes that the solution is reduced to the sequential solutions to several systems called local. These systems have the property of ellipticity, that is, such equations resemble diffusion equations without a fractional degree. Such systems are well solved numerically. However, when the approximate solution to the original problem as a whole needs to be "assembled" from the obtained solutions, the pieces do not always "fit together" well—the solution obtained sometimes approximates the solution to the original problem accurately, and sometimes it differs greatly.
Petr Vabishchevich and his colleague chose another way, reducing the solution to the fractional diffusion equation to several local systems. The resulting systems did not possess the ellipticity property and were even worse, in a sense. Moreover, the system included functions with discontinuities, which usually means low solvability for numerical problems. But in this particular case, it turned out that the correct choice of the time step for the calculation, together with a good choice of the system itself, allows obtaining a numerical solution that quite accurately approximates the solution to the original problem.
Moreover, it appears that the method proposed by RUDN University mathematicians often works faster than its counterparts. This is because the transition to an approximate solution occurs at the last step in the new scheme. In other methods, the approximation occurs in several stages, which leads to the accumulation of calculation errors. This does not occur with the new method.
The fractional diffusion equations describe the so-called anomalous diffusion, e.g., the distribution of a liquid in a porous medium with discontinuities. In addition, fractional diffusion describes the transfer of nutrients within a cell and in tissues in general. These equations in general form are not solvable, therefore, scientists use numerical approximations, that is, approximate solutions. The RUDN University mathematicians' new method will allow performing calculations faster in many cases.
More information: Raimondas Čiegis et al. Two-level schemes of Cauchy problem method for solving fractional powers of elliptic operators, Computers & Mathematics with Applications (2019). DOI: 10.1016/j.camwa.2019.08.012
Provided by RUDN University