Mathematicians proposed an express method for calculation of the propagation of light
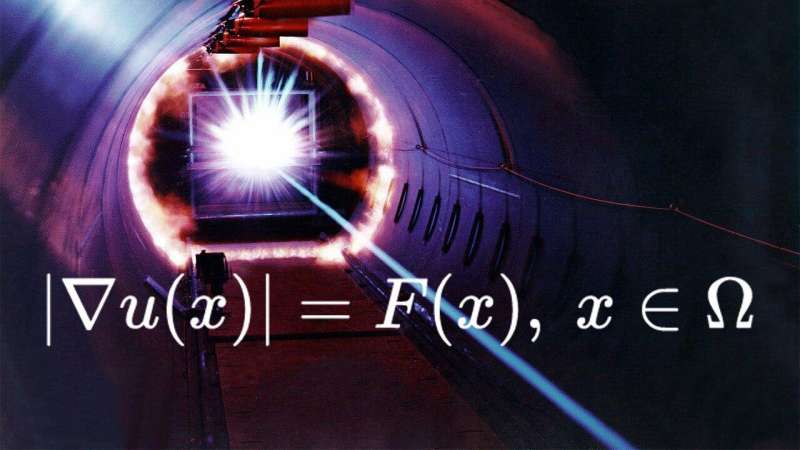
Mathematicians from RUDN University and the Nuclear Safety Institute of the RAS (NSI RAS) have proposed a numerical method for solving equations describing the propagation of light in a medium. They used the nonlinear eikonal equation with boundary conditions as the basis. Such a problem cannot be solved directly, so the mathematicians developed a numerical method, performed calculations, and produced a picture of the "behavior" of such solutions. The results could become the basis for a comprehensive theory of approximate solutions of such differential equations. The method can be applied in the production of lenses and optical crystals. The article was published in the Journal of Computational and Applied Mathematics.
The eikonal equation is a nonlinear partial differential equation. It describes the propagation of light in a medium and is necessary for solving problems in optics. It makes it possible to connect planar optics, taught in schools, and wave optics, which is described by complex equations.
It is traditional to use a method based on solving a large system of nonlinear equations to find a numerical solution (i.e., to obtain a sufficiently accurate approximate solution) for the eikonal equation.
RUDN University and NSI RAS mathematicians used a different approach, which makes it easier to find a solution for the nonlinear eikonal equation using a numerical method: a change of variables with the addition of a parameter. The change results in new equations, which, on the one hand, are simpler than the initial ones: the problem becomes linear. On the other hand, their solutions are not the solutions of the original system. However, as the parameter decreases the solutions for the new system get closer to the solutions for the original one.
Mathematicians gradually (by a certain fixed value) decreased the value of the added parameter and for each such value solved the equation numerically. For each subsequent parameter value the resulting solution was compared with the previous ones. As the parameter decreased the solutions changed less and less, that is, the result of the calculations stabilized. It turned out that a sufficiently stable solution requires a relatively small parameter value. The resulting solution was taken as an approximation of the original equation.
The mathematicians have demonstrated that such a method produces fairly good results on representative model problems.
"Computational complexity—the so-called 'computational costs' of the approach we are talking about—does not exceed that of other approaches. Although, we solve a linear boundary value problem, and that, of course, is less laborious than solving a nonlinear problem," explained Petr Vabishevich, the author of the study and a member of the Research Center for Computational Methods in Applied Mathematics of the RUDN University.
Vabishevich and his co-authors modeled the equation for anisotropic media. From the point of view of physics, this is an environment in which the physical properties of light propagation in different directions are not the same. Materials with these properties are now widely used in optical devices.
Besides optics, the eikonal equation is also used to numerically solve equations describing the motion of a fluid. Such modeling is necessary to create realistic pictures in computer graphics—for example, in the film "Pirates of the Caribbean" the water was not just drawn but calculated on a physical level. The speed of calculation, which could potentially be improved by the method developed by mathematicians at RUDN University and NSI RAS, plays a key role in such cases.
More information: Alexander G. Churbanov et al. Numerical solution of boundary value problems for the eikonal equation in an anisotropic medium, Journal of Computational and Applied Mathematics (2019). DOI: 10.1016/j.cam.2019.05.016
Provided by RUDN University