Speeding up artificial intelligence
A group at Politecnico di Milano has developed an electronic circuit able to solve a system of linear equations in a single operation in the timescale of a few tens of nanoseconds. The performance of this new circuit is superior not only to classical digital computers, but also to quantum computers. It will be soon possible to develop a new generation of computing accelerators that will revolutionize the technology of artificial intelligence.
Solving a system of linear equations means finding the unknown vector X which satisfies the equation Ax = b, where A is a matrix of coefficients and b is a known vector. To solve this problem, a conventional digital computer executes an algorithm that takes several operations, thus translating into considerable time and energy consumption.
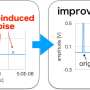
The new circuit, which has been developed in the frame of the ERC European project Resistive Switch Computing Beyond CMOS (RESCUE), solves systems of linear equations (Ax=b) thanks to an innovative method of in-memory computing, where the coefficients of matrix A are stored in a special device called a memristor. The memristor is able to store analogue values, so a memristor matrix can physically map a coefficient matrix A within the circuit, thus strongly accelerating the computation.
The memristor circuit has been tested and validated on a wide set of algebraic problems, such as the ranking of internet websites and the solution of complicated differential equations including the Schrödinger equation for the computation of the quantum wavefunction for an electron. All these problems are solved in a single operation.
These results have been published in the Proceedings of the National Academy of Science.
More information: Zhong Sun et al. Solving matrix equations in one step with cross-point resistive arrays, Proceedings of the National Academy of Sciences (2019). DOI: 10.1073/pnas.1815682116
Journal information: Proceedings of the National Academy of Sciences
Provided by Politecnico di milano