February 12, 2020 feature
Time crystals and topological superconductors merge

"Powering a topological superconductor using a time crystal gives you more than the sum of its parts," says Jason Alicea, a researcher at California Institute of Technology (Caltech) in the US. The discovery of topological states has bred reams of research revealing new condensed matter and quantum physics, with potential technological applications in spintronics and quantum computing. Similarly, not long after the first observations of topological insulators in the late 2000s, the concepts of time crystals emerged, introducing another fresh arena for exploring new physics that could be exploited in precise timekeeping and quantum technologies.
Now, Alicea, alongside Aaron Chew, also at Caltech, and David Mross at the Weizmann Institute in Israel, report in Physical Review Letters theoretical investigations of systems that merge the two phenomena. "The intertwinement between time crystallinity and topological physics generates an interesting twist on excitations that are being pursued for fault-tolerant quantum computing," adds Alicea.
What are topological materials?
The researchers were fortunate to stumble on these systems as something of a "happy accident" during studies Chew and Mross were conducting on topological superconductors, one type of a whole family of materials that has proliferated fruitfully over the past 10 to 20 years. The theory of topological materials is based on the concept of properties of topologies (such as the shape of a doughnut or sphere) that are invariant under smooth transformations. A typical example of such smooth transformations is the morphing of a doughnut into a coffee cup—the sphere cannot morph into a doughnut or a coffee cup without making a cut for the hole or handle, which would make the transformation no longer smooth.
In a topological insulator, properties associated with the electron wave function are topologically invariant. What makes them interesting is the interface between topological and ordinary insulators. In crossing this boundary, the wave function has to undergo a change that can lead to conducting edge or surface states at the boundary that are symmetry-protected by particle number conservation and time-reversal symmetry, making them particularly robust to perturbations. This could allow for sturdier qubits, for example.

Since the first observation of a 2-D topological insulator in 2007, 3-D topological states have come to light in which intrinsic spin-orbit coupling takes the place of the magnetic field, as well as topological superconductors and photonic and magnetic analogues. Catalogues have since emerged revealing the near-ubiquity of topological materials in nature. The extraordinary fertility of this field led to the award of the 2016 Nobel Prize for Physics to David J. Thouless, F. Duncan M. Haldane, and J. Michael Kosterlitz "for theoretical discoveries of topological phase transitions and topological phases of matter."
What are time crystals?
Around 2012, considerations of systems that have the same kind of periodicity in time as is observed in space in conventional crystals raised interest in the idea of time crystals—"neat phases of matter that physicists have learned a lot about just over the past several years," Alicea tells Phys.org. In a conventional crystal, a continuous translational symmetry is broken in the lowest energy state, giving way to a discrete periodic symmetry. When viewing time as a fourth coordinate of space-time, it seems natural to look for such symmetry breaking in time, as well. However, defining time crystals simply in terms of this symmetry breaking runs into problems with ambiguities in terms of energy, as well as oscillations in some trivial systems that would render the designation "time crystal" meaningless.
In a recent review by Vedika Khemani at Harvard and Stanford University in the U.S., Roderich Moessner at Max-Planck-Institut für Physik komplexer Systeme in Germany and Shivaji Sondhi at Princeton in the U.S., time crystals were more restricted. The term only applied to locally bounded Hamiltonian systems with non-trivial time dependence over asymptotically long times that meet additional requirements on the initial conditions to define a phase of matter with translational time symmetry breaking. This limits the Hamiltonian systems that can give rise to time crystals to many-body localized and periodically driven so-called Floquet systems.
What links the two?
Chew and Mross were particularly interested in "non-Abelian anyons" that can exist in topologically ordered phases. An anyon is a particle that is neither strictly a fermion nor a boson, while non-Abelian refers to behaviour that can be described in terms of operations that lead to different results depending on the order. A classical example of "non-commutating" operations might be a rotation through 90 degrees about one axis and then a perpendicular axis.
In superconducting systems, quasiparticles exist known as Majorana fermions, a type of fermion that is its own antiparticle as first hypothesized by Ettore Majorana in 1937. When bound to a defect, the resulting zero-energy Majorana modes have non-Abelian statistics that could provide the anyon building blocks of a topological quantum computer with qubits that are much more stable than those based on trapped quantum particles.
Chew and Mross were investigating how to establish a link between non-Abelian defects in 2-D topologically ordered phases and those that can arise in strictly 1-D fermion systems. Alicea explains that the study led them to the discovery that it is possible to enrich topological superconductors by coupling them to controllable magnetic degrees of freedom. "Then we realized that by turning those magnetic degrees of freedom into a time crystal, topological superconductivity responds in remarkable ways," says Alicea.
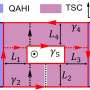
Time-crystalline topological superconductors
In their latest work, Alicea, Chew and Mross consider coupling the Cooper electron pairs in a 1-D topological superconductor to time-crystalline Ising spins, where the Ising spins flip after each period. Since it takes two periods for the Ising spins to reach their original state, they are considered doubled-periodicity time-crystalline Ising spins.
If a 1-D free-fermion topological superconductor hosting Majorana end modes is periodically driven, "Floquet Majorana modes" appear, carrying energy related to half the driving frequency. In one of the observations from their analysis of time-crystalline topological superconductors, Alicea, Chew and Mross reveal quadrupled periodicity in "Floquet Majorana modes." They also propose experimental schemes for implementing and detecting these systems.
"It's tempting to imagine generating some useful quantum operations by controlling the magnetic degrees of freedom that intertwine with the topological physics. Or perhaps certain noise channels can be suppressed by exploiting time crystals," says Alicea. Future work may investigate whether these systems can also occur in 2-D and 3-D materials. "The existence of time crystals, however, is a subtle topic outside of 1-D," Alicea adds. "It's still interesting, though, to ask whether one can realize higher-dimensional analogues of our 1-D time-crystalline topological superconductor. They might only live for a finite time, but that time might be sufficiently long to observe new physics."
More information: Aaron Chew et al. Time-crystalline topological superconductors Physical Review Letters (2020). journals.aps.org/prl/accepted/ … 2600efeed0fb1530ecd4 , arxiv.org/abs/1907.12570
Journal information: Physical Review Letters
© 2020 Science X Network