Indeterminist physics for an open world

Classical physics is characterized by the precision of its equations describing the evolution of the world as determined by the initial conditions of the Big Bang—meaning there is no room for chance. Yet our day-to-day experience and intuition are struck by this deterministic vision of the world: has everything really been written in advance? Is randomness nothing more than an illusion? A physicist from UNIGE, Swizerland, has been analyzing the classical mathematical language used in modern physics. He has thrown light on a contradiction between the equations that are supposed to explain the phenomena that surround us and the finite world. He suggests making changes to the mathematical language to allow randomness and indeterminism to become part of classical physics, thereby bringing it closer to quantum physics. Thanks to these observations, which are published in the journal Nature Physics, a revolution is sweeping through classical physics and paving the way for potentially different futures.
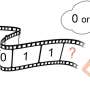
In classical physics, or Newton's physics, it is accepted that everything has already been determined since the Big Bang. The evolution of the world is explained by mathematical equations that describe the world as unfolding from these initial conditions in the most precise way. For this, physicists employ the language of classical mathematics and represent these initial conditions by real numbers. "These numbers are characterized by an infinite number of decimals that follow the dot," says Nicolas Gisin, professor emeritus at the Department of Applied Physics, UNIGE's Faculty of Science and the author of the observation. "This implies that they contain an infinite amount of information." Such typical real numbers are far more numerous than numbers that have a name, such as Pi, and consist of a series of decimals that are completely random. We do not encounter them in everyday life but their existence is an accepted postulate in classical maths and they are used in many equations in physics. There is a problem, however: given that our world is finite, how can it include numbers that are infinite and that feature an infinite amount of information?
Leaving the language of classical mathematics behind for the language of intuitionistic mathematics
To circumvent the impossibility that the finite contains the infinite, professor Gisin suggests going back to the source of classical physics and changing the mathematical language so that we no longer have to resort to real numbers. "There is another mathematical language, called intuitionistic, which doesn't believe in the existence of the infinite," continues the Geneva physicist. "But it was completely crushed by the classic mathematical language at the beginning of the twentieth century." Instead of real numbers containing an infinite number of decimals at a given moment, intuitionistic mathematics represents these numbers as a random process that takes place over time, one decimal after the other, so that at each given moment there is only a finite number of decimals, and—it follows—a finite amount of information. " This solves the contradiction of classical physics, which uses infinity to explain the finite," adds professor Gisin.
There is another difference between the two mathematical languages: the truth of propositions. "In classical maths, a proposition is always either true or false, according to the law of excluded middle. But in intuitionistic maths, a proposition is either true, false or indeterminate. So, there is an accepted part of indeterminacy," continues professor Gisin. This indeterminacy is much closer to our everyday experience than the most absolute determinism advocated by classical physics. In addition, randomness is also found in quantum physics. "Some people endeavor to avoid it at all costs by involving other variables based on real numbers. But in my opinion, we shouldn't try to bring quantum physics closer to classical physics by attempting to eliminate randomness. Quite the opposite: we must bring classical physics closer to quantum physics by finally incorporating indeterminacy," says the Geneva-based physicist.
Open physics based on intuition instead of postulates
Our vision of the world is constructed via the language we speak. If we choose the language of classical mathematics, we will talk easily about determinism. If, on the contrary, we choose the language of intuitionistic mathematics, we will easily move towards indeterminism. "I now consider that we have accepted too many postulates in classical physics, meaning we have integrated a form of determinism that wasn't necessarily on any ground. On the other hand, if we choose to base classical physics on intuitionistic mathematics, it will also become indeterminate, like quantum physics, and will be closer to our actual experience, opening up possibilities for our future," explains professor Gisin.
"This change of language wouldn't change the results of research conducted to date but it would make it easier to understand quantum physics and eventually to abandon a worldview where everything is already written, making room for new perspectives, randomness, chance and creativity," concludes professor Gisin.
More information: Nicolas Gisin. Mathematical languages shape our understanding of time in physics, Nature Physics (2020). DOI: 10.1038/s41567-019-0748-5
Journal information: Nature Physics
Provided by University of Geneva