Mathematicians prove the Hardy-Littlewood-Sobolev inequalities

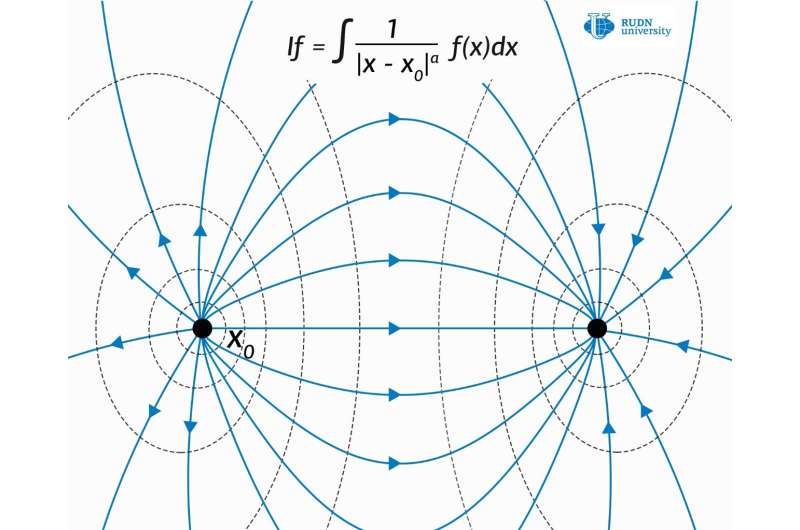
RUDN University mathematicians have proven the Hardy-Littlewood-Sobolev (HLS) inequalities for the class of generalized Riesz potentials. These results extend the scope of these potentials in mathematics and physics because the main tools for working with such potentials are based on HLS inequalities. New mathematical tools can greatly simplify calculations in quantum mechanics and other fields of physics. The results of the study are published in the journal Mathematical Notes.

Modern physics describes the world in terms of fields and their potentials—that is, the values of the field at each point. But the physical quantities that we can measure are forces and accelerations, that is, derivatives of the second-order of the potential of the corresponding field. The problem of reconstructing the field configuration with the available values of forces and accelerations observed in experiments is complex and not always analytically solvable. Differentiation operations in multidimensional space—operators are usually used to describe the correlation between the potential of the field and the forces. In particular, electromagnetic and gravitational interactions are described in the language of operators.

Since the potential of the field can be determined up to a constant value, for the convenience of calculations, the initial value of the potential is taken at some point in multidimensional space, or on the border of any spatial area. But in some cases, mathematical models of such fields lead to a singularity, that is, at some points the value of the field becomes infinite, and therefore loses its physical meaning.

Vagif Guliyev, the researcher of the Nikol'skii Institute of Mathematics of RUDN University, and his colleagues worked on the development of methods that allow restoring the configuration of the field potential using only analytical methods.

RUDN University mathematicians studied one of the important cases for the development of quantum theory—the necessary and sufficient conditions for the boundedness of the Riesz potential generated by the Gegenbauer differential operator in weighted Lebesgue spaces Lp,λ. Their study develops and complements the earlier proof of the Hardy-Littlewood-Sobolev theorem for the Gegenbauer potential.

Operators defined by Riesz potentials have many applications in physics—Riesz potentials include, for example, electrostatic potential.

The proof of the Hardy-Littlewood-Sobolev inequality for generalized Riesz potentials means that physicists and mathematicians have a tool which will help them to determine in advance, before carrying out laborious calculations, whether it is possible to analytically calculate the configuration of the field with the available values of forces, and not to obtain a singularity.

The results of the study can be used in physics to determine the conditions under which it is possible to restore the spatial picture of physical fields of different nature, for example, in the field of quantum electrodynamics.