June 4, 2019 feature
Training neural belief-propagation decoders for quantum error-correcting codes
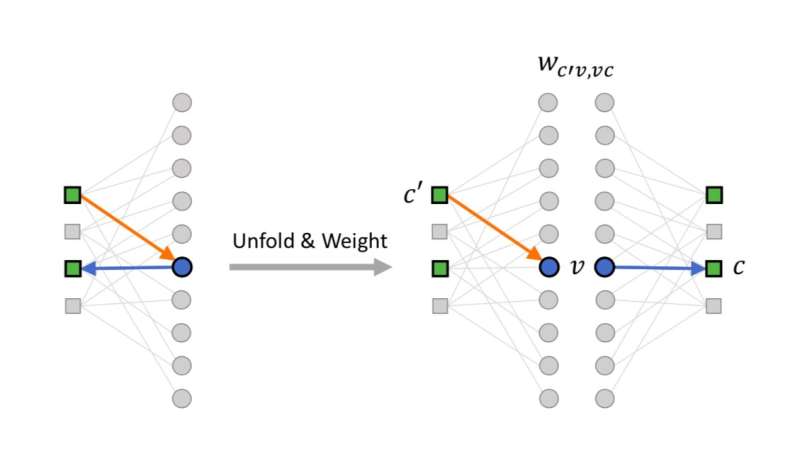
Two researchers at Université de Sherbrooke, in Canada, have recently developed and trained neural belief-propagation (BP) decoders for quantum low-density parity-check (LDPC) codes. Their study, outlined in a paper published in Physical Review Letters, suggests that training can enhance the performance of BP decoders significantly, helping to solve issues that are commonly associated with their application in quantum research.
"Ten years ago, I wrote an article with Yeojin Chung explaining how standard decoding algorithms for LDPC codes, which are broadly used in classical communication, would fail in the quantum setting," David Poulin, one of the researchers who carried out the study, told Phys.org. "This problem has been obsessing me ever since. Recently, people have started to investigate the use of neural networks to decode quantum codes, but they all focused on a problem (decoding topological codes) that already had a number of good human-designed solutions. This was the perfect occasion to revisit my favorite open problem and use neural networks to decode quantum codes that had no previously known decoder."
While BP decoders are commonly applied in a variety of settings, so far they have proved to be unsuitable for decoding quantum error-correcting codes. This is due to a unique quantum feature referred to as 'error degeneracy," which essentially means that there are multiple ways to correct an error in quantum settings.
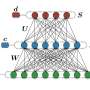
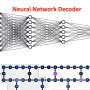
Classical BP algorithms consist of of three simple equations. The structure of these equations enables an exact mapping to a feed-forward neural network. In other words, it is possible to reinterpret the BP equations commonly used to decode LDPC codes as describing the initial setting of a neural network.
Past research has found that this 'initial neural network' does not work well in quantum settings, despite achieving better performance than random neural networks. In their study, Poulin and his colleague Ye-Hua Liu enhanced the performance of the 'initial neural network' by training it with data generated by numerical simulations.
"The training is guided by a target function that takes into account quantum effects," Liu told Phys.org. "Generally speaking, neural decoders have the advantage that they are adaptive to arbitrary noise statistics in realistic channels. In addition to that, our method is applicable to quantum LDPC codes without regular lattice structures. These codes are very promising for realizing low-overhead quantum error correction."
The researchers found that training the neural BP decoders using the technique they adopted improved their performance, for all the families of LDPC codes they tested. Moreover, the training technique they used could help to solve the degeneracy problem that generally plagues the decoding of quantum LDPC codes.
"Training the neural BP network can significantly improve its performance for quantum error correction, which means a classical algorithm can be adapted to the quantum setting by deep-learning methods," Liu said. "This inspires us to look for other examples like this in quantum physics, to reveal a broader connection between deep learning and natural science. For instance, belief propagation is widely used in many other research areas, including statistical physics, which implies neural BP might also benefit research in quantum statistical physics."
In their future work, Poulin and Liu plan to study neural BP in the context of statistical physics. If trained using the same technique, the researchers expect that BP, which is also referred to as the 'cavity method' in this particular setting, will show an improved performance in this context too.
"More broadly, belief propagation belongs to the important class of message-passing algorithms, which turns out to be closely related to graph convolutional networks in deep-learning research," Liu added. "It would be very fruitful to gain insights into these structures from a physicist's point of view."
More information: Ye-Hua Liu et al. Neural Belief-Propagation Decoders for Quantum Error-Correcting Codes, Physical Review Letters (2019). DOI: 10.1103/PhysRevLett.122.200501
David Poulin, Yeojin Chung. On the iterative decoding of sparse quantum codes. arXiv:0801.1241 [quant-ph]. arxiv.org/abs/0801.1241
Journal information: Physical Review Letters
© 2019 Science X Network