June 21, 2019 feature
Climbing droplets driven by mechanowetting on transverse waves
Modern applications use self-cleaning strategies and digital microfluids to control individual droplets of fluids on flat surfaces but existing techniques are limited by the side-effects of high electric fields and high temperatures. In a new study, Edwin De Jong and co-workers at the interdisciplinary departments of Advanced Materials, Mechanical Engineering and Complex Molecular Systems developed an innovative "mechanowetting" technique to control droplet motion on changing surfaces based on the interfacial surface tension.
To demonstrate the method, they transported droplets using transverse waves on horizontal and vertically inclined surfaces at velocities equal to the speed of the wave. The scientists captured the fundamental mechanism of the mechanowetting force in theory and quantitatively to establish the phenomenon's dependence on the properties of the fluid, surface energy and wave parameters. Jong et al. demonstrated "mechanowetting" as a technique that can lead to a range of new applications featuring droplet control through surface deformations. The research is now published on Science Advances.
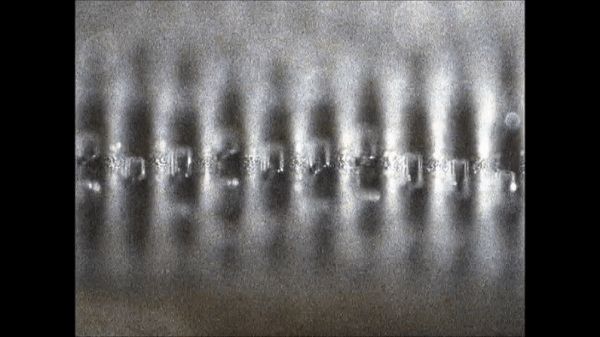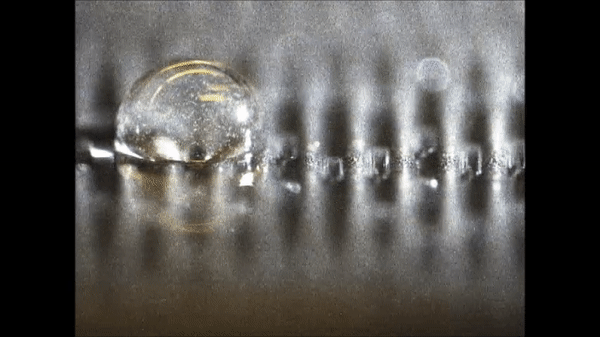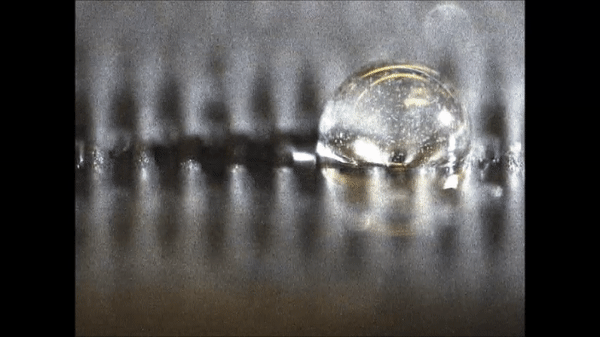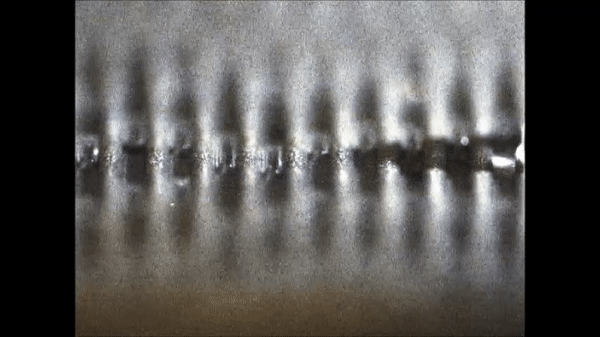
In the work, Jong et al. quantified the dynamic pinning forces that drove mechanowetting by studying the climbing droplets of diverse sizes on varying angles of inclination. They observed unexpectedly large forces and were able to drive droplets even against vertical walls at substantial speeds. The droplets were able to pick contaminating particles along the way to demonstrate their potential in self-cleaning applications. The scientists captured the underlying mechanisms of droplet transport numerically and in theory to establish its dependence on multiple physical parameters. Jong et al. expect the technique to drive a range of new applications based on three-phase line manipulation of the contact angle and by switching surface topographies.
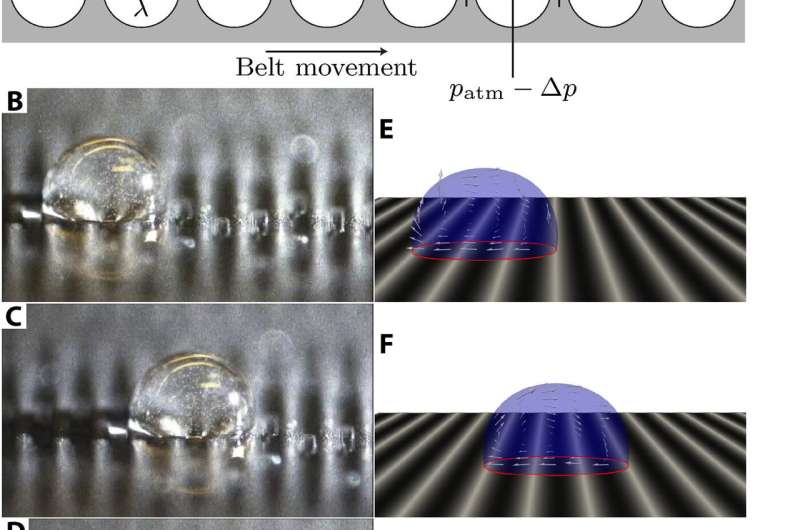
The scientists built a device to generate regular and controllable transverse surface waves to experimentally demonstrate droplet transport. In its mechanism of action, they lowered the pressure underneath a film made of polydimethylsiloxane (PDMS) clamped by a metal frame to create a wave-like surface architecture to ensure purely transverse waves. Using the experimental setup, the scientists controlled droplets ranging from 0.1 to 5 µL on transverse waves accounting to a wavelength of 500 nm traveling at a speed of 0.57 mm/s; equal to the speed of the applied wave. The materials scientists carried out a combination of computational fluid dynamics (CFD) simulations, theoretical modeling and single-droplet experiments to numerically analyze the individual droplets.
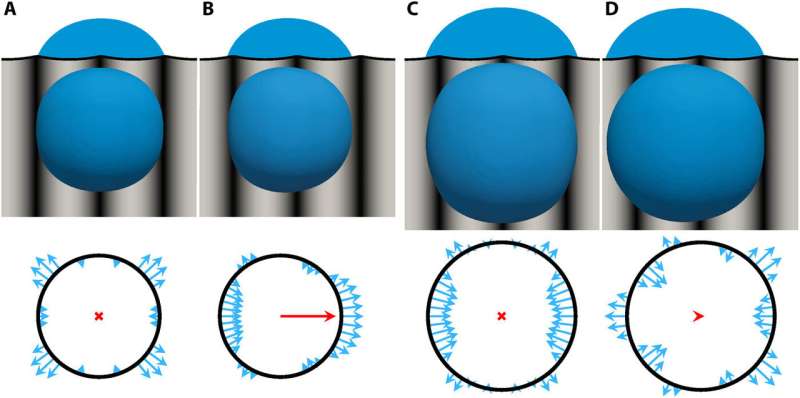
During the computational modeling experiments, they developed an openFOAM framework to create a simulation that agreed excellently with the experiments. To understand the effectiveness of the droplet transport mechanism, the scientists conducted a series of climbing droplet experiments and simulations with the device tilted at an angle of interest. Jong et al. showed that when the driving force for the bigger droplet was larger than the gravitational force, the droplet climbed upward, whereas with smaller droplets the greater gravitational force caused the droplets to slide down.
![Droplet transport on inclined surfaces. (A) Critical angle βcrit as a function of the droplet size d normalized by the wavelength λ. The markers are experimental results; error bars represent the SD of at least three measurements. The trend line corresponds to numerical results. The numerical model uses the experimental settings as input, i.e., the Young angle θY = 68°, wavelength λ = 500 μm, amplitude A = 4.0 ± 1.0 μm, and the dynamic viscosity ν = 1 mm2 s−1 of the fluid (water-isopropanol). The error margin in the amplitude is reflected by the shaded area around the main trend line (in orange). (B and C) Two-droplet experiment showing droplets of size d/λ = 2.7 and 3.1 at inclination angle β = 13° [corresponding to the marked locations in (A) indicated by the dashed lines]. The arrows indicate the droplet movement. (D) Numerical results depicting the change in critical angle βcrit as a function of wave speed uwave and wave amplitude A for a droplet of size d/λ = 3.2 (λ = 500 μm). The marked data point corresponds to the amplitude and wave speed of the experiments shown in (A). Credit: Science Advances, doi: 10.1126/sciadv.aaw0914 Climbing droplets driven by mechanowetting on transverse waves](https://scx1.b-cdn.net/csz/news/800a/2019/1-climbingdrop.jpg)
During the experiments the scientists identified a "restoring force" that drove droplet motion and quantified this by modeling the droplet as a spherical cap. They showed the dynamic-pinning force that balanced the counteracting forces, which included static pinning, gravity and viscous forces during droplet transport.
They obtained the highest forces that could be generated in the setup for contact angles near 65.5 degrees. In addition, the droplets on the traveling waves could overcome considerable gravitational forces to even climb up vertical surfaces at a velocity of 0.57 mm/s. Jong et al. showed millimeter-sized droplets that could be transported upside down; to demonstrate phenomena that had hitherto lacked experimental demonstration.
During the in vitro (in lab) experiments, the scientists formed the traveling wave device using a conveyor belt constructed using electric discharge machining with built-in speed control mounted in a vacuum chamber. They affixed the PDMS film made by spin-coating onto an aluminum frame placed on top of the exposed part of this belt. The low pressure created in the device allowed the PDMS film to be pressed against the belt and the scientists controlled the wave amplitude by controlling the pressure level inside the chamber.
They tested the mechanism using several fluids including water, isopropanol and mineral oil to show the method as a robust, consistent and reproducible process to move droplets for all cases. Jong et al. verified this efficacy by spraying droplets of varying sizes simultaneously on the traveling wave. The observed versatility of mechanowetting was remarkable compared to previous methods with special requirements. When they explored the self-cleaning properties of the constructed traveling mechanowetting surface, the researchers found the droplets' ability to wipe the surface clean from contamination. The technique allowed controlled droplet motion to collect debris at designated locations, unlike previous self-cleaning processes based on rigid and static hydrophobic surfaces.

In this way, Jong et al. experimentally demonstrated climbing droplet motion on mechanowetting surfaces and emphasized a requisite topographical deformation at the surface three-phase line to influence the balance of local surface tension and achieve motion. The present setup is limited as an experimental proof-of-concept device on the mechanism of mechanowetting. The scientists aim to optimize the system and build devices which will feature topographies that can mechanically deform in response to external stimuli including light, magnetic fields and temperature. They can also control splitting and merging droplets by creating surfaces with two traveling waves that travel toward or away from each other.
Edwin Jong and co-workers believe that mechanowetting can be fully explored to open new opportunities for high-precision droplet handling in a variety of medical and industrial applications based on the method detailed in the study. Droplets driven by mechanowetting will find future applications in microfluidics for diagnostics and cell handling/analysis and as self-cleaning devices in medicine, in marine sensors, windows and solar panels, while also finding applications in dew harvesting.
More information: Edwin De Jong et al. Climbing droplets driven by mechanowetting on transverse waves, Science Advances (2019). DOI: 10.1126/sciadv.aaw0914
Helen Song et al. Reactions in Droplets in Microfluidic Channels, Angewandte Chemie International Edition (2006). DOI: 10.1002/anie.200601554
Ali Hashmi et al. Leidenfrost levitation: beyond droplets, Scientific Reports (2012). DOI: 10.1038/srep00797
M. K. Chaudhury et al. How to Make Water Run Uphill, Science (2006). DOI: 10.1126/science.256.5063.1539
Journal information: Science Advances , Angewandte Chemie International Edition , Scientific Reports , Science
© 2019 Science X Network