New theory deepens understanding of Turing patterns in biology

A team of researchers at EMBL have expanded Alan Turing's seminal theory on how patterns are created in biological systems. This work, which was partly done at the Centre for Genomic Regulation (CRG), may answer whether nature's patterns are governed by Turing's mathematical model and could have applications in tissue engineering. Their results have been published on 20 June in Physical Review X.
Alan Turing sought to explain how patterns in nature arise with his 1952 theory on morphogenesis. The stripes of a zebra, the arrangement of fingers and the radial whorls in the head of a sunflower, he proposed, are all determined through a unique interaction between molecules spreading out through space and chemically interacting with each other. Turing's famous theory can be applied to various fields, from biology to astrophysics.
Many biological patterns have been proposed to arise according to Turing's rules, but scientists have not yet been able to provide a definitive proof that these biological patterns are governed by Turing´s theory. Theoretical analysis also seemed to predict that Turing systems are intrinsically very fragile, unlikely for a mechanism that governs patterns in nature.
Going beyond Turing's theory
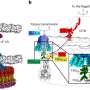
Xavier Diego, James Sharpe and colleagues from EMBL's new site in Barcelona analysed computational evidence that Turing systems can be much more flexible than previously thought. Following this hint, the scientists, based at the CRG and are now at EMBL, expanded Turing's original theory by using graph theory, a branch of mathematics that studies the properties of networks and makes it easier to work with complex, realistic systems. This led to the realization that network topology, the structure of the feedback between the networks' components, is what determines many fundamental properties of a Turing system. Their new topological theory provides a unifying view of many crucial properties for Turing systems that were previously not well understood and explicitly defines what is required to make a successful Turing system.
A Turing system consist of an activator that must diffuse at a much slower rate than an inhibitor to produce a pattern. The majority of Turing models require a level of parameter fine-tuning that prevents them from being a robust mechanism for any real patterning process. "We learned that studying a Turing system through the topological lens really simplifies the analysis. For example, understanding the source of the diffusion restrictions becomes straightforward, and more importantly, we can easily see what modifications are needed to relax these restrictions," explains Xavier Diego, first author of the paper.
"Our approach can be applied to general Turing systems, and the properties will be true for networks with any number of components. We can now predict if the activity in two nodes in the network is in or out of phase, and we also found out which changes are necessary to switch this around. This allows us to build networks that make any desired pair of substances overlap in space, which could have interesting applications in tissue engineering."
Turing hieroglyphs for experimental groups
The researchers also provide a pictorial method that enables researchers to easily analyse existing networks or to come up with new network designs. "We call them 'Turing hieroglyphs' in the lab," says EMBL Barcelona group leader James Sharpe, who led the work. "By using these hieroglyphs, we hope that our methods will be adopted by both theoreticians and by experimental groups that are trying to implement Turing networks in biological cells."
This expanded theory provides experimental research groups with a new approach to making biological cells develop in patterns in the lab. If experimental groups are successful in this, the questions over whether Turing's theory of morphogenesis applies to biological systems will finally be answered.
More information: Diego, X., et al. Key features of Turing systems are determined purely by network topology. Physical Review X, published online 20 June 2018.
Journal information: Physical Review X
Provided by European Molecular Biology Laboratory