May 31, 2017 feature
Physicists uncover similarities between classical and quantum machine learning
(Phys.org)—Physicists have found that the structure of certain types of quantum learning algorithms is very similar to their classical counterparts—a finding that will help scientists further develop the quantum versions. Classical machine learning algorithms are currently used for performing complex computational tasks, such as pattern recognition or classification in large amounts of data, and constitute a crucial part of many modern technologies. The aim of quantum learning algorithms is to bring these features into scenarios where information is in a fully quantum form.
The scientists, Alex Monràs at the Autonomous University of Barcelona, Spain; Gael Sentís at the University of the Basque Country, Spain, and the University of Siegen, Germany; and Peter Wittek at ICFO-The Institute of Photonic Science, Spain, and the University of Borås, Sweden, have published a paper on their results in a recent issue of Physical Review Letters.
"Our work unveils the structure of a general class of quantum learning algorithms at a very fundamental level," Sentís told Phys.org. "It shows that the potentially very complex operations involved in an optimal quantum setup can be dropped in favor of a much simpler operational scheme, which is analogous to the one used in classical algorithms, and no performance is lost in the process. This finding helps in establishing the ultimate capabilities of quantum learning algorithms, and opens the door to applying key results in statistical learning to quantum scenarios."
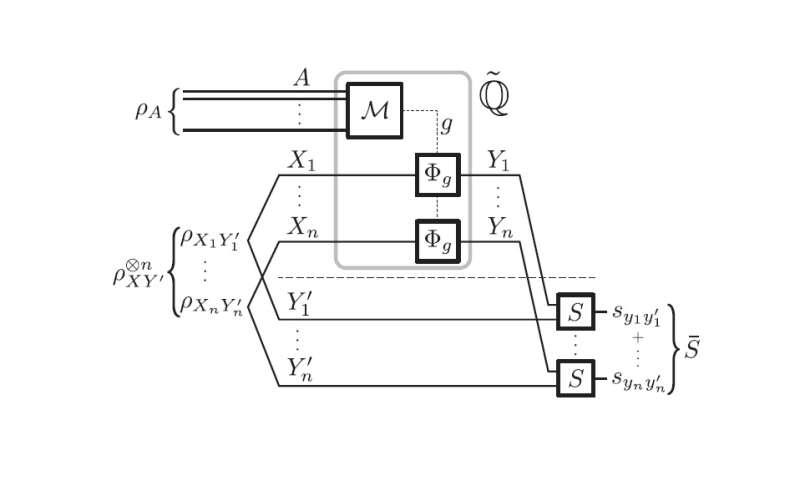
In their study, the physicists focused on a specific type of machine learning called inductive supervised learning. Here, the algorithm is given training instances from which it extracts general rules, and then applies these rules to a variety of test (or problem) instances, which are the actual problems that the algorithm is trained for. The scientists showed that both classical and quantum inductive supervised learning algorithms must have these two phases (a training phase and a test phase) that are completely distinct and independent. While in the classical setup this result follows trivially from the nature of classical information, the physicists showed that in the quantum case it is a consequence of the quantum no-cloning theorem—a theorem that prohibits making a perfect copy of a quantum state.
By revealing this similarity, the new results generalize some key ideas in classical statistical learning theory to quantum scenarios. Essentially, this generalization reduces complex protocols to simpler ones without losing performance, making it easier to develop and implement them. For instance, one potential benefit is the ability to access the state of the learning algorithm in between the training and test phases. Building on these results, the researchers expect that future work could lead to a fully quantum theory of risk bounds in quantum statistical learning.
"Inductive supervised quantum learning algorithms will be used to classify information stored in quantum systems in an automated and adaptable way, once trained with sample systems," Sentís said. "They will be potentially useful in all sorts of situations where information is naturally found in a quantum form, and will likely be a part of future quantum information processing protocols. Our results will help in designing and benchmarking these algorithms against the best achievable performance allowed by quantum mechanics."
More information: Alex Monràs et al. "Inductive Supervised Quantum Learning." Physical Review Letters 118, 190503. DOI: 10.1103/PhysRevLett.118.190503
Journal information: Physical Review Letters
© 2017 Phys.org