New algorithm cuts through 'noisy' data to better predict tipping points
Whether you're trying to predict a climate catastrophe or mental health crisis, mathematics tells us to look for fluctuations.
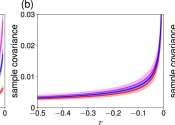
Whether you're trying to predict a climate catastrophe or mental health crisis, mathematics tells us to look for fluctuations.
Mathematics
13 hours ago
0
88

A new algorithm is making it easier for ecologists and conservationists to find bat roost locations—reducing search areas by nearly 375 times their previous size. The technology combines microphone detector data with a ...
Ecology
Apr 24, 2024
0
10

An algorithm developed by a Florida Tech graduate student creates a new ecological survey method that allows scientists to unlock important historical data from a vast trove of coral-reef photographs dating back more than ...
Ecology
Apr 23, 2024
0
40
Though "coupled oscillations" may not sound familiar, they are everywhere in nature. The term "coupled harmonic oscillators" describes interacting systems of masses and springs, but their utility in science and engineering ...
Quantum Physics
Apr 22, 2024
0
95

An international research collaboration between Vanderbilt University and the Madrid-based de la Prida lab in the Cajal Institute led to the development of AI models that detect and analyze hippocampal ripples, which are ...
Biotechnology
Apr 18, 2024
0
29

In the rugged terrain of the western United States, where wildfires rage unchecked, a surprising connection emerges with the tumultuous skies of the central US. A recent study published in Advances in Atmospheric Sciences ...
Earth Sciences
Apr 11, 2024
0
6

Algorithms were supposed to make our lives easier and fairer: help us find the best job applicants, help judges impartially assess the risks of bail and bond decisions, and ensure that health care is delivered to the patients ...
Social Sciences
Apr 9, 2024
0
49

Researchers have developed a 3D full-color display method that uses a smartphone screen rather than a laser to create holographic images. With further development, the new approach could be useful for augmented or virtual ...
Optics & Photonics
Apr 2, 2024
0
99

Ph.D. candidate Jeroen Methorst has developed a computer system that helps researchers find the protein they need to create new medicines. "Our whole group is now using this program," says Methorst. He will defend his Ph.D. ...
Molecular & Computational biology
Mar 27, 2024
0
12

Imagine a world where complex calculations that currently take months for our best supercomputers to crack could be performed in a matter of minutes. Quantum computing is revolutionizing our digital world. In a research article ...
Quantum Physics
Mar 25, 2024
0
55
In mathematics, computing, linguistics, and related subjects, an algorithm is a finite sequence of instructions, an explicit, step-by-step procedure for solving a problem, often used for calculation and data processing. It is formally a type of effective method in which a list of well-defined instructions for completing a task, will when given an initial state, proceed through a well-defined series of successive states, eventually terminating in an end-state. The transition from one state to the next is not necessarily deterministic; some algorithms, known as probabilistic algorithms, incorporate randomness.
A partial formalization of the concept began with attempts to solve the Entscheidungsproblem (the "decision problem") posed by David Hilbert in 1928. Subsequent formalizations were framed as attempts to define "effective calculability" (Kleene 1943:274) or "effective method" (Rosser 1939:225); those formalizations included the Gödel-Herbrand-Kleene recursive functions of 1930, 1934 and 1935, Alonzo Church's lambda calculus of 1936, Emil Post's "Formulation 1" of 1936, and Alan Turing's Turing machines of 1936–7 and 1939.
This text uses material from Wikipedia, licensed under CC BY-SA