Another step toward understanding of high-temperature superconductivity

(Phys.org) —Superconductors can radically change energy management as we know it, but most are commercially unusable because they only work close to absolute zero. A research group at EPFL has now published an innovative approach that may help us understand and use superconductivity at more realistic temperatures.
Superconductors are materials that allow electrical current to flow with no energy loss, a phenomenon that can lead to a vastly energy-efficient future (imagine computers that never overheat). Although most superconductors work close to absolute zero (0°K or -273.15°C), some can operate at higher temperatures (around -135°C) – but how that happens is something of a mystery. Publishing in a recent PNAS article, Fabrizio Carbone's Laboratory for Ultrafast Microscopy and Electron Scattering (LUMES) at EPFL has developed a method that can shed light on "high-temperature" superconductivity.
How conventional superconductivity works
When electricity passes through a conductor, e.g. a wire, some energy is lost because of resistance. This is not always a bad thing, since it can be used for heat (radiators) or light (light bulbs). But when it comes to things like national energy grids and high-voltage cables, electrical resistance (up to 7% in some grids) can mean money and constant wear.
This is where superconductors come in. These are materials that, when cooled down enough, conduct electricity with no resistance – and therefore no loss. How? As superconductors cool below a certain temperature, their atoms fall in line and "nudge" charge-carrying electrons together to make new particles called Cooper pairs. These electron pairs observe quantum physics and form an unusual state of matter (a Bose-Einstein Condensate) that is not affected by electrical resistance.
Superconductors can revolutionize the way we use and distribute energy, change modes of transportation (e.g. Japan's magnetic levitation trains) and give us 100% energy-efficient technology. So why hasn't that happened yet? The problem is temperature: Most superconductors only work when they are cooled close to the forbidding absolute zero. The solution lies with those that work at higher temperatures.
A new method for exploring high-temperature superconductivity
Recently, the lab of Fabrizio Carbone at EPFL addressed the issue by developing a novel method that can advance our understanding of high-temperature superconductivity. High-temperature superconductors (HTS) show promise because they can operate at temperatures around -135°C – still low, but considerably cheaper and more feasible than for conventional superconductors. However, progress in HTS is limited because, even though we know that Cooper pairs are involved in high-temperature superconductivity, there is no consensus as to how they are formed.
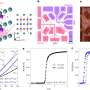
Carbone's group was able, for the first time, to directly observe the formation of Cooper pairs in real time in a superconducting HTS and determine how the process affects the optical properties of the superconductor. Using a novel approach, the scientists cooled an HTS to its superconducting temperature and then repeatedly fired laser pulses on it to break up the Cooper pairs back into single electrons. As the Cooper pairs broke and re-formed, they caused a periodical change in the color spectrum of the superconductor. By measuring the color change, the researchers were able to directly study what happens in a superconducting HTS. What they discovered was that Cooper pair formation follows a completely different path than in conventional superconductors.
Carbone's findings mark the first direct observation of Cooper pair formation in HTS superconductivity. They also provide scientists with a powerful tool to observe the phenomenon in real time. The hope is that by extending this innovative approach to different materials, we can begin to understand how high-temperature superconductivity really works.
More information: Coupling of a high-energy excitation to superconducting quasiparticles in a cuprate from coherent charge fluctuation spectroscopy, www.pnas.org/content/110/12/4539.abstract
Journal information: Proceedings of the National Academy of Sciences
Provided by Ecole Polytechnique Federale de Lausanne