Superconductivity's third side unmasked
The debate over the mechanism that causes superconductivity in a class of materials called the pnictides has been settled by a research team from Japan and China. Superconductivity was discovered in the pnictides only recently, and they belong to the class of so-called 'high-temperature superconductors'. Despite their name, the temperature at which they function as superconductors is still well below room temperature. Realizing superconductivity at room temperature remains a key challenge in physics; it would revolutionize electronics since electrical devices could operate without losing energy.
Superconductivity in a material arises when two electrons bind together into so-called Cooper pairs. This pairing leads to a gap in the energy spectrum of the superconducting material, which makes the electrons insensitive to the mechanisms causing electrical resistance. Electrons can bind into Cooper pairs in different ways, leading to different categories of superconductors.
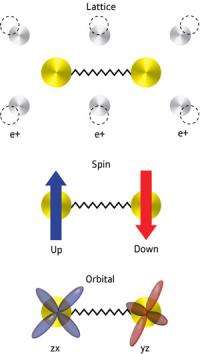
Until the work of Takahiro Shimojima from The University of Tokyo and his colleagues, including researchers from the RIKEN SPring-8 Center in Harima, superconducting materials were classified into two broad categories. In classical superconductors, which function at very low temperatures, vibrations of atoms in the crystal lattice of the material provide the necessary glue for the pairing. In cuprates, the original high-temperature superconductor compounds, magnetic interactions based on an electron’s spin generate the superconductive pairing (Fig. 1). In the pnictide high-temperature superconductors, physicists assumed that the underlying mechanism was similar to that for the cuprates, but conflicting experimental results meant that the precise mechanism was controversial.
To investigate this debated pairing mechanism of pnictides, the researchers studied the properties of the material’s electronic gap. Thanks to a unique set of high-energy lasers based on very rare laser crystals available to only a few laboratories, their experiments resolved these states with unprecedented detail.
Shimojima and colleagues were surprised to discover that interactions between electron spins do not cause the electrons to form Cooper pairs in the pnictides. Instead, the coupling is mediated by the electron clouds surrounding the atomic cores. Some of these so-called orbitals have the same energy, which causes interactions and electron fluctuations that are sufficiently strong to mediate superconductivity.
This could spur the discovery of new superconductors based on this mechanism. “Our work establishes the electron orbitals as a third kind of pairing glue for electron pairs in superconductors, next to lattice vibrations and electron spins,” explains Shimojima. “We believe that this finding is a step towards the dream of achieving room-temperature superconductivity,” he concludes.
More information: Shimojima, T., Sakaguchi, F., Ishizaka, K., Ishida, Y., Kiss, T., Okawa, M., Togashi, T., Chen, C.-T., Watanabe, S., Arita, M., et al. Orbital-independent superconducting gaps in iron-pnictides. Science published online 7 April 2011 (doi: 10.1126/science.1202150).
Provided by RIKEN