Study proposes a mathematical model to study malaria transmission
Malaria affects over 200 million individuals every year and kills hundreds of thousands of people worldwide. The disease varies greatly from region to region in the species that cause it and in the carriers that spread it. It is easily transmitted across regions through travel and migration. This results in outbreaks of the disease even in regions that are essentially malaria-free, such as the United States. Malaria has been nearly eliminated in the U.S. since the 1950s, but the country continues to see roughly 1,500 cases a year, most of them from travelers. Hence, the movement or dispersal of populations becomes important in the study of the disease.
In a paper published this month in the SIAM Journal on Applied Mathematics, authors Daozhou Gao and Shigui Ruan propose a mathematical model to study malaria transmission.
"Malaria is a parasitic vector-borne disease caused by the plasmodium parasite, which is transmitted to people via the bites of infected female mosquitoes of the genus Anopheles," says Ruan. "It can be easily transmitted from one region to another due to extensive travel and migration."
The life cycle of plasmodium involves incubation periods in two hosts, the human and the mosquito. Therefore, mathematical modeling of the spread of malaria usually focuses on the feedback dynamics from mosquito to human and back. Early models were based on malaria parasites' population biology and evolution. But increased computing power in recent years has allowed models for the disease to become more detailed and complex.
Mathematical models that study transmission of malaria are based on the "reproduction number," which defines the most important aspects of transmission for any infectious disease. Specifically, it is calculated by determining the expected number of infected organisms that can trace their infection directly back to a single organism after one disease generation. The solution to controlling the disease is to arrive at a reproduction number at which the disease-free state can be established and maintained.
Previous studies used ordinary differential equations to model the transmission of malaria, in which human populations are classified as susceptible, exposed, infectious and recovered. Likewise, mosquito populations are divided into susceptible, exposed and infectious groups. The threshold below which the disease-free equilibrium can be maintained is determined by varying these parameters.
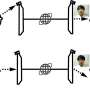
In order to analyze transmission rates of malaria between regions, multi-patch models are used, where each region is a "patch." These models study how the reproduction number is affected by dispersal or movement of exposed and infectious individuals from region to region.
The authors in this paper model the transmission dynamics of malaria between humans and mosquitoes within a patch, and then go on to examine how population dispersal between patches or regions affects the spread of malaria in a two-patch model.
After deriving the reproduction number, they determine its dependence on human travel rates. Their analysis shows that reproduction number varies consistently with movement of exposed, infectious and recovered humans. The same is seen to be true for the movement of infected mosquitoes. "A threshold for the persistence of malaria was obtained, below which the disease dies out and above which the disease persists," explains Ruan. "Analysis of the threshold helps us design effective control measures to reduce disease transmission."
The authors determine that malaria can potentially die out if movement of exposed, infectious or recovered humans between two patches or regions remains weak; higher travel rates between the patches, however, can make malaria indigenous to both regions. Numerical simulations are performed to corroborate these findings.
The paper thus concludes that human travel is a critical factor affecting the spread of malaria. "The analytical and numerical results confirm that human movement plays a significant role in the geographic spread of malaria among different regions," says Ruan. Anti-malaria measures should involve more rigorous border screening and regulation, since exposed individuals who don't exhibit symptoms of the disease—but are infectious—are hard to identify at screenings. "To control malaria, both regional and global strategies are needed," he says.
Future directions for this research include testing the global stability of this model in more than two patches, and studying other influencers, such as climate. "Climate factors such as rainfall and temperature greatly influence the abundance and distribution of malaria vectors," Ruan says. "It will be very interesting to study the impact of climate change on the transmission of malaria by considering periodic malaria models."
More information: A Multipatch Malaria Model with Logistic Growth Populations, Shigui Ruan and Daozhou Gao, SIAM Journal on Applied Mathematics, 72(3), 819-841. (Online publish date: June 7, 2012)
Journal information: SIAM Journal on Applied Mathematics
Provided by Society for Industrial and Applied Mathematics