January 27, 2014 feature
Nanoscale heat engine exceeds standard efficiency limit
(Phys.org) —In 2012, a team of physicists from Germany proposed a scheme for realizing a nanoscale heat engine composed of a single ion. Like a macroscale heat engine, the theoretical nanoscale version can convert heat into mechanical work by taking advantage of the temperature difference between two thermal reservoirs. Because the single-ion heat engine is so small, at the time the physicists noted that it had the potential to tap into the quantum regime and experience quantum effects.
Now in a new paper, the physicists, from the Universities of Mainz and Erlangen-Nürnberg in Germany, have theoretically shown that a nanoscale heat engine can take advantage of nonthermal effects.
"Our theoretical and numerical findings show that the performance of quantum heat engines may be enhanced by coupling them to engineered nonthermal reservoirs, like squeezed reservoirs," coauthor Eric Lutz, Physics Professor at the University of Erlangen-Nürnberg, told Phys.org. "These results follow from the application of the second law of thermodynamics to a reservoir configuration that is more general than usually considered in textbooks. From a theoretical point of view, they indicate that the second law is less restrictive away from equilibrium."
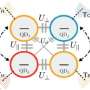
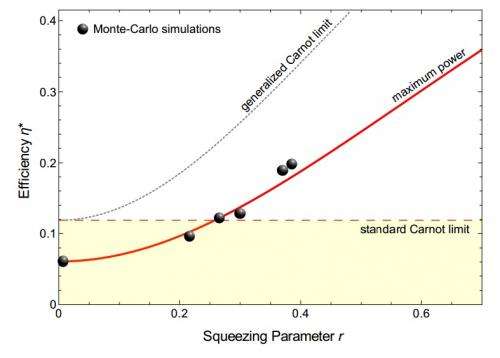
In their paper, the physicists showed that when the high-temperature thermal reservoir to which the quantum heat engine is attached is "squeezed," the heat engine's efficiency at maximum power dramatically increases and can exceed the standard Carnot limit by a factor of two. Since the power of an engine vanishes at maximum efficiency, the efficiency at maximum power is the quantity of prime interest for practical applications.
As an expression of the second law of thermodynamics, Carnot's result places a fundamental limit on a heat engine's maximum efficiency. However, this limit holds only for the particular configuration that involves two thermal reservoirs at different temperatures.
The engine proposed here has only one thermal reservoir, since the reservoir that is squeezed is considered nonthermal. While thermal reservoirs are characterized only by their temperatures, nonthermal reservoirs can be controlled in additional ways, such as by squeezing.
As the physicists explain, squeezing is a quantum optics concept that has been shown to be a useful tool in high-precision spectroscopy, quantum information, quantum cryptography, and other areas. However, the use of squeezed thermal reservoirs in quantum thermodynamics has been largely unexplored until now.
The physicists' simulations showed that this heat engine can be experimentally realized with current technology involving a single ion and laser reservoirs. The simulations revealed that such a heat engine could realistically operate at maximum power with an efficiency that is up to four times larger than the efficiency obtained with two thermal reservoirs, and a factor of two above the standard Carnot limit.
In the future, these dramatic improvements in efficiency through squeezing could lead to the realization of more efficient nanoengines.
"We succeeded recently to trap ions and plan to verify the predicted results in the lab," Lutz said. "We are currently investigating heat pumps and the options to scale the number of ions up."
More information: J. Roßnagel, et al. "Nanoscale Heat Engine Beyond the Carnot Limit." Physical Review Letters. DOI: 10.1103/PhysRevLett.112.030602
Also available at arXiv:1308.5935 [quant-ph]
Journal information: Physical Review Letters
© 2014 Phys.org. All rights reserved.