Testing Einstein's E=mc2 in outer space
(Phys.org)—University of Arizona physicist Andrei Lebed has stirred the physics community with an intriguing idea yet to be tested experimentally: The world's most iconic equation, Albert Einstein's E=mc2, may be correct or not depending on where you are in space.
With the first explosions of atomic bombs, the world became witness to one of the most important and consequential principles in physics: Energy and mass, fundamentally speaking, are the same thing and can, in fact, be converted into each other.
This was first demonstrated by Albert Einstein's Theory of Special Relativity and famously expressed in his iconic equation, E=mc2, where E stands for energy, m for mass and c for the speed of light (squared).
Although physicists have since validated Einstein's equation in countless experiments and calculations, and many technologies including mobile phones and GPS navigation depend on it, University of Arizona physics professor Andrei Lebed has stirred the physics community by suggesting that E=mc2 may not hold up in certain circumstances.
The key to Lebed's argument lies in the very concept of mass itself. According to accepted paradigm, there is no difference between the mass of a moving object that can be defined in terms of its inertia, and the mass bestowed on that object by a gravitational field. In simple terms, the former, also called inertial mass, is what causes a car's fender to bend upon impact of another vehicle, while the latter, called gravitational mass, is commonly referred to as "weight."
This equivalence principle between the inertial and gravitational masses, introduced in classical physics by Galileo Galilei and in modern physics by Albert Einstein, has been confirmed with a very high level of accuracy. "But my calculations show that beyond a certain probability, there is a very small but real chance the equation breaks down for a gravitational mass," Lebed said.
If one measures the weight of quantum objects, such as a hydrogen atom, often enough, the result will be the same in the vast majority of cases, but a tiny portion of those measurements give a different reading, in apparent violation of E=mc2. This has physicists puzzled, but it could be explained if gravitational mass was not the same as inertial mass, which is a paradigm in physics.
"Most physicists disagree with this because they believe that gravitational mass exactly equals inertial mass," Lebed said. "But my point is that gravitational mass may not be equal to inertial mass due to some quantum effects in General Relativity, which is Einstein's theory of gravitation. To the best of my knowledge, nobody has ever proposed this before."
Lebed presented his calculations and their ramifications at the Marcel Grossmann Meeting in Stockholm last summer, where the community greeted them with equal amounts of skepticism and curiosity. Held every three years and attended by about 1,000 scientists from around the world, the conference focuses on theoretical and experimental General Relativity, astrophysics and relativistic field theories. Lebed's results will be published in the conference proceedings in February.
In the meantime, Lebed has invited his peers to evaluate his calculations and suggested an experiment to test his conclusions, which he published in the world's largest collection of preprints at Cornell University Library (see More Info).
"The most important problem in physics is the Unifying Theory of Everything – a theory that can describe all forces observed in nature," said Lebed. "The main problem toward such a theory is how to unite relativistic quantum mechanics and gravity. I try to make a connection between quantum objects and General Relativity."
The key to understand Lebed's reasoning is gravitation. On paper at least, he showed that while E=mc2 always holds true for inertial mass, it doesn't always for gravitational mass.
"What this probably means is that gravitational mass is not the same as inertial," he said.
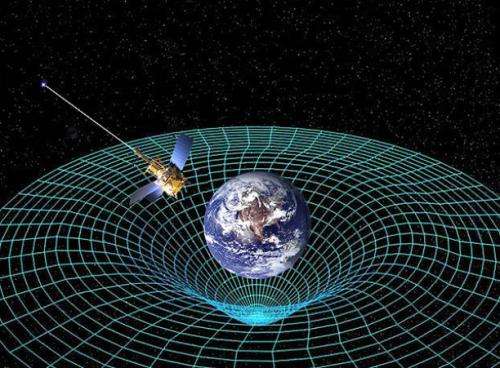
According to Einstein, gravitation is a result of a curvature in space itself. Think of a mattress on which several objects have been laid out, say, a ping pong ball, a baseball and a bowling ball. The ping pong ball will make no visible dent, the baseball will make a very small one and the bowling ball will sink into the foam. Stars and planets do the same thing to space. The larger an object's mass, the larger of a dent it will make into the fabric of space.
In other words, the more mass, the stronger the gravitational pull. In this conceptual model of gravitation, it is easy to see how a small object, like an asteroid wandering through space, eventually would get caught in the depression of a planet, trapped in its gravitational field.
"Space has a curvature," Lebed said, "and when you move a mass in space, this curvature disturbs this motion."
According to the UA physicist, the curvature of space is what makes gravitational mass different from inertial mass.
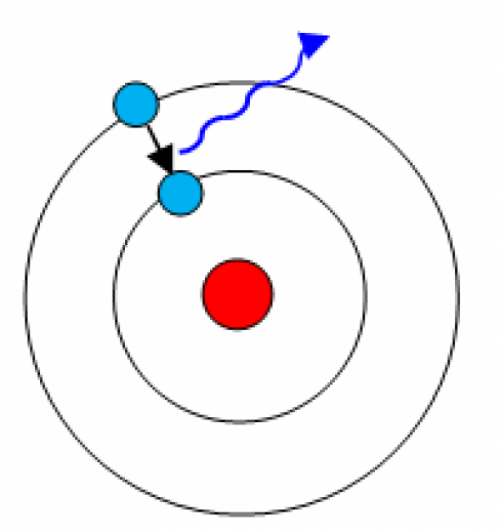
Lebed suggested to test his idea by measuring the weight of the simplest quantum object: a single hydrogen atom, which only consists of a nucleus, a single proton and a lone electron orbiting the nucleus.
Because he expects the effect to be extremely small, lots of hydrogen atoms would be needed.
Here is the idea:
On a rare occasion, the electron whizzing around the atom's nucleus jumps to a higher energy level, which can roughly be thought of as a wider orbit. Within a short time, the electron falls back onto its previous energy level. According to E=mc2, the hydrogen atom's mass will change along with the change in energy level.
So far, so good. But what would happen if we moved that same atom away from Earth, where space is no longer curved, but flat?
You guessed it: The electron could not jump to higher energy levels because in flat space it would be confined to its primary energy level. There is no jumping around in flat space.
"In this case, the electron can occupy only the first level of the hydrogen atom," Lebed explained. "It doesn't feel the curvature of gravitation."
"Then we move it close to Earth's gravitational field, and because of the curvature of space, there is a probability of that electron jumping from the first level to the second. And now the mass will be different."
"People have done calculations of energy levels here on Earth, but that gives you nothing because the curvature stays the same, so there is no perturbation," Lebed said. "But what they didn't take into account before that opportunity of that electron to jump from the first to the second level because the curvature disturbs the atom."
"Instead of measuring weight directly, we would detect these energy switching events, which would make themselves known as emitted photons – essentially, light," he explained.
Lebed suggested the following experiment to test his hypothesis: Send a small spacecraft with a tank of hydrogen and a sensitive photo detector onto a journey into space.
In outer space, the relationship between mass and energy is the same for the atom, but only because the flat space doesn't permit the electron to change energy levels.
"When we're close to Earth, the curvature of space disturbs the atom, and there is a probability for the electron to jump, thereby emitting a photon that is registered by the detector," he said.
Depending on the energy level, the relationship between mass and energy is no longer fixed under the influence of a gravitational field.
Lebed said the spacecraft would not have to go very far.
"We'd have to send the probe out two or three times the radius of Earth, and it will work."
According to Lebed, his work is the first proposition to test the combination of quantum mechanics and Einstein's theory of gravity in the solar system.
"There are no direct tests on the marriage of those two theories," he said. " It is important not only from the point of view that gravitational mass is not equal to inertial mass, but also because many see this marriage as some kind of monster. I would like to test this marriage. I want to see whether it works or not."
More information: The details of Andrei Lebed's calculations are published in three preprint papers with Cornell University Library:
xxx.lanl.gov/abs/1111.5365
xxx.lanl.gov/abs/1205.3134
xxx.lanl.gov/abs/1208.5756
Provided by University of Arizona