Q&A: Expert explains the 'physics of AI'

The development of a new theory is typically associated with the greats of physics. You might think of Isaac Newton or Albert Einstein, for example. Many Nobel Prizes have already been awarded for new theories.

Researchers at Forschungszentrum Jülich have now programmed an artificial intelligence that has also mastered this feat. Their AI is able to recognize patterns in complex data sets and to formulate them in a physical theory. The findings are published in the journal Physical Review X.

In the following interview, Prof. Moritz Helias from Forschungszentrum Jülich's Institute for Advanced Simulation (IAS-6) explains what the "Physics of AI" is all about and to what extent it differs from conventional approaches.

How do physicists come up with a new theory?

You usually start with observations of the system before attempting to propose how the different system components interact with each other in order to explain the observed behavior. New predictions are then derived from this and put to the test.

A well-known example is Isaac Newton's law of gravitation. It not only describes the gravitational force on Earth, but it can also be used to predict the movements of planets, moons, and comets—as well as the orbits of modern satellites—fairly accurately.

However, the way in which such hypotheses are reached always differs. You can start with general principles and basic equations of physics and derive the hypothesis from them, or you can choose a phenomenological approach, limiting yourself to describing observations as accurately as possible without explaining their causes. The difficulty lies in selecting a good approach from the numerous approaches possible, adapting it if necessary, and simplifying it.

What approach are you taking with AI?

In general, it involves an approach known as "physics for machine learning." In our working group, we use methods of physics to analyze and understand the complex function of an AI.

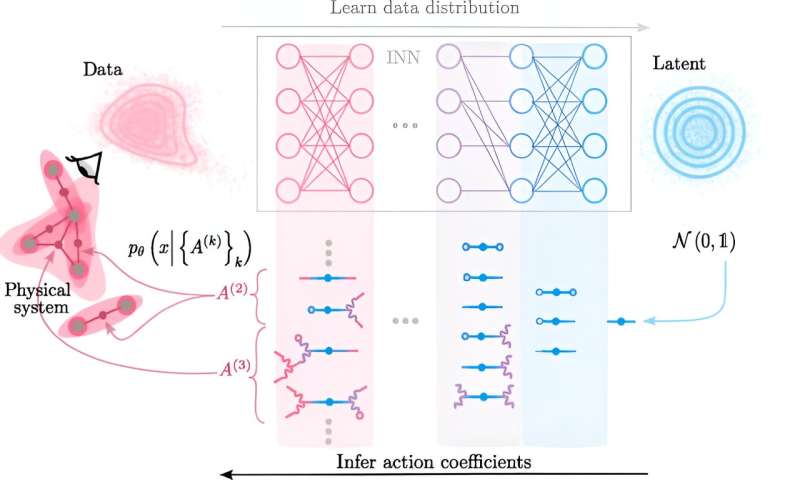
The crucial new idea developed by Claudia Merger from our research group was to first use a neural network that learns to accurately map the observed complex behavior to a simpler system. In other words, the AI aims to simplify all the complex interactions we observe between system components. We then use the simplified system and create an inverse mapping with the trained AI. Returning from the simplified system to the complex one, we then develop the new theory.

On the way back, the complex interactions are built up piece by piece from the simplified ones. Ultimately, the approach is therefore not so different from that of a physicist, with the difference being that the way in which the interactions are assembled is now read from the parameters of the AI. This perspective on the world—explaining it from interactions between its various parts that follow certain laws—is the basis of physics, hence the term "physics of AI."

In which applications was AI used?

We used a data set of black and white images with handwritten numbers, for example, which is often used in research when working with neural networks. As part of her doctoral thesis, Claudia Merger investigated how small substructures in the images, such as the edges of the numbers, are made up of interactions between pixels. Groups of pixels are found that tend to be brighter together and thus contribute to the shape of the edge of the number.

How high is the computational effort?

The use of AI is a trick that makes the calculations possible in the first place. You very quickly reach a very large number of possible interactions. Without using this trick, you could only look at very small systems. Nevertheless, the computational effort involved is still high, which is due to the fact that there are many possible interactions even in systems with many components.

However, we can efficiently parameterize these interactions so that we can now view systems with around 1,000 interacting components, i.e., image areas with up to 1,000 pixels. In the future, much larger systems should also be possible through further optimization.

How does this approach differ from other AIs such as ChatGPT?

Many AIs aim to learn a theory of the data used to train the AI. However, the theories that the AIs learn usually cannot be interpreted. Instead, they are implicitly hidden in the parameters of the trained AI. In contrast, our approach extracts the learned theory and formulates it in the language of interactions between system components, which underlies physics.

It thus belongs to the field of explainable AI, specifically the "physics of AI," as we use the language of physics to explain what the AI has learned. We can use the language of interactions to build a bridge between the complex inner workings of AI and theories that humans can understand.