A mathematical framework for evo-devo dynamics

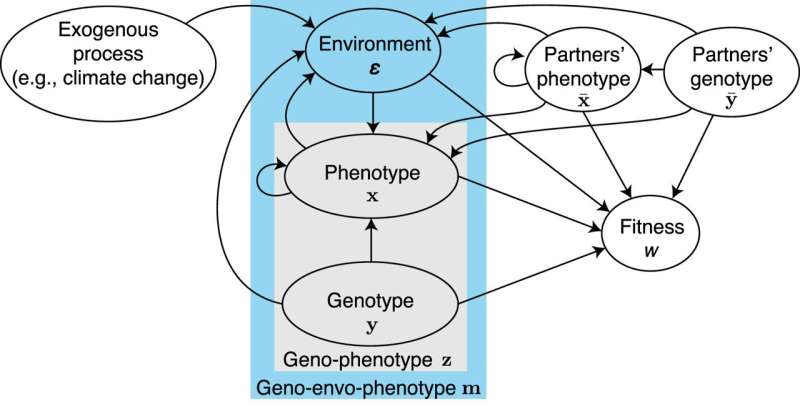
Natural selection acts on phenotypes constructed over development, which raises the question of how development affects evolution.

Classic evolutionary theory indicates that development affects evolution by modulating the genetic covariation upon which selection acts, thus affecting genetic constraints. However, whether genetic constraints are relative, thus diverting adaptation from the direction of steepest fitness ascent, or absolute, thus blocking adaptation in certain directions, remains uncertain.

This limits the understanding of long-term evolution of developmentally constructed phenotypes. In a paper published in the journal Theoretical Population Biology, researchers formulate a general, tractable mathematical framework that integrates age progression, explicit development (i.e., the construction of the phenotype across life subject to developmental constraints), and evolutionary dynamics, thus describing the evolutionary and developmental (evo-devo) dynamics.

The framework yields simple equations that can be arranged in a layered structure that they call the evo-devo process, whereby five core elementary components generate all equations including those mechanistically describing genetic covariation and the evo-devo dynamics.

The framework recovers evolutionary dynamic equations in gradient form and describes the evolution of genetic covariation from the evolution of genotype, phenotype, environment, and mutational covariation.

This shows that genotypic and phenotypic evolution must be followed simultaneously to yield a dynamically sufficient description of long-term phenotypic evolution in gradient form, such that evolution described as the climbing of a fitness landscape occurs in "geno-phenotype" space.

Genetic constraints in geno-phenotype space are necessarily absolute because the phenotype is related to the genotype by development.

Thus, the long-term evolutionary dynamics of developed phenotypes is strongly non-standard:

1. Evolutionary equilibria are either absent or infinite in number and depend on genetic covariation and hence on development
2. Developmental constraints determine the admissible evolutionary path and hence which evolutionary equilibria are admissible
3. Evolutionary outcomes occur at admissible evolutionary equilibria, which do not generally occur at fitness landscape peaks in geno-phenotype space, but at peaks in the admissible evolutionary path where "total genotypic selection" vanishes if exogenous plastic response vanishes and mutational variation exists in all directions of genotype space.

Hence, selection and development jointly define the evolutionary outcomes if absolute mutational constraints and exogenous plastic response are absent, rather than the outcomes being defined only by selection.

Moreover, the framework provides formulas for the sensitivities of a recurrence and an alternative method to dynamic optimization (i.e., dynamic programming or optimal control) to identify evolutionary outcomes in models with developmentally dynamic traits. These results show that development has major evolutionary effects.