This article has been reviewed according to Science X's editorial process and policies. Editors have highlighted the following attributes while ensuring the content's credibility:
fact-checked
peer-reviewed publication
trusted source
proofread
New possibilities in the theoretical prediction of particle interactions
How does the world look like at the smallest scales? This is a question scientists are trying to answer in particle collider experiments like the Large Hadron Collider at CERN in Switzerland. To compare the results of these experiments, theoretical physicists need to provide more and more precise predictions based on our current model for the interactions of fundamental particles, the so called standard model.
A key ingredient in these predictions are so called Feynman integrals. Recently, a team of the PRISMA+ Cluster of Excellence at Mainz University, consisting of Dr. Sebastian Pögel, Dr. Xing Wang and Prof. Dr. Stefan Weinzierl developed a method to efficiently compute a new class of these Feynman integrals, associated to Calabi–Yau geometries.
This research is now published in the journal Physical Review Letters and opens the path to high-precision theoretical predictions of particle interactions, and to better understand the elegant mathematical structure underpinning the world of particle physics.
"During the interaction of subatomic particles something special happens: Any number of additional particles can temporarily pop in and out of existence," Prof. Dr. Stefan Weinzierl explains. "When making theoretical predictions of such interactions, the more of the these additional particles are taken into account, the more precise the computation will be to the real result." Feynman integrals are mathematical objects which describe this effect, summing in effect all possible ways particles can appear and immediately disappear again.
Calabi–Yau geometries: An interplay of mathematics and physics
An important property determining the complexity of a Feynman integral is its geometry. Many of the simplest Feynman integrals have the geometry of a sphere or a torus—the mathematical term for a donut shape. Such integrals are nowadays well understood. However, there exist entire families of geometries, so-called Calabi–Yau geometries, which are generalizations of the donut case to higher dimensions.
These have proven to be a rich field of research in pure Mathematics, and have found extensive application in string theory in the last decades. In recent years it was discovered that many Feynman integrals are also associated to Calabi–Yau geometries. However, due to the complexity of the geometry, the efficient evaluation of such integrals has remained a challenge.
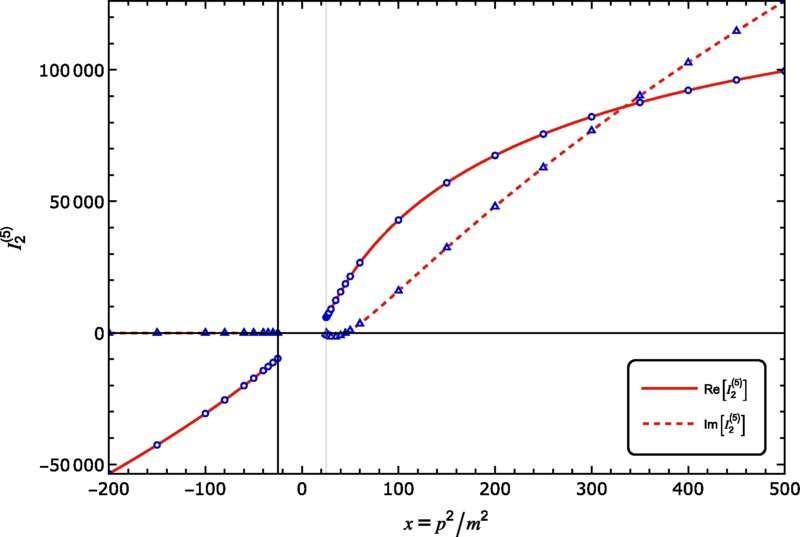
In their recent publication, Dr. Sebastian Pögel, Dr. Xing Wang and Prof. Dr. Stefan Weinzierl present a method that allows them to tackle integrals of Calabi–Yau geometries. In their research they studied a simple family of Calabi–Yau Feynman integrals, called banana integrals. The name is derived from the Feynman graph. Thereby they could find for the first time a so-called "epsilon-factorized form" for these integrals.
This form allows them to quickly evaluate the integral to nearly arbitrary precision, making them accessible for future experimental predictions. "It opens the door to a wide variety of hitherto unreachable Feynman integrals," says Dr. Xing Wang. According to Dr. Sebastian Pögel it is a nice example of how pure mathematics feeds into phenomenological predictions for high-energy experiments.
"We are grateful to our colleagues in mathematics, and in particular to the group of Prof. Dr. Duco van Straten, as we build on their work and now were able to achieve this exciting result," says Prof. Dr. Stefan Weinzierl.
More information: Sebastian Pögel et al, Taming Calabi-Yau Feynman Integrals: The Four-Loop Equal-Mass Banana Integral, Physical Review Letters (2023). DOI: 10.1103/PhysRevLett.130.101601
Journal information: Physical Review Letters
Provided by Universitaet Mainz